Математический анализ функции одной переменной: Учебное пособие. Часть 1 (Элементы математической логики. Множества чисел. Комплексные числа. Производная функции. Дифференциал), страница 12

При попытке найти пределы для числителя и знаменателя дроби по отдельности получаем:

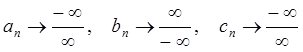, то есть во всех трех случаях возникает одно и то же соотношение неопределенности . Раскроем соотношение неопределенности для каждой из последовательностей, для этого подойдем к задаче нахождения пределов более аккуратно, рассматривая числители и знаменатели дробей одновременно. 

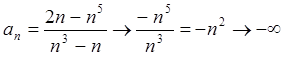
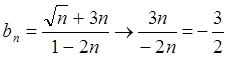
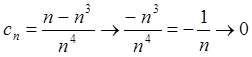
Как мы видим, неопределенность  после раскрытия может оказаться любым отрицательным числом, нулем или символом  в зависимости от конкретного вида последовательности.

10. Ряды

Определение 1: Сумму нескольких подряд расположенных членов последовательности , начиная с  и заканчивая , будем обозначать

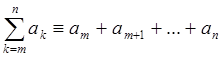.                                                    (51)

Частичной суммой ряда  называется сумма первых  членов последовательности

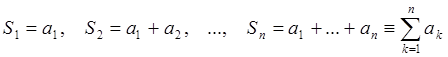.                              (52)

Определение 2: Говорят, что бесконечный ряд сходится, если существует (конечный) предел последовательности его частичных сумм

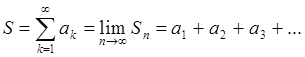                                             (53)

Число  называют суммой ряда. Если предела последовательности частичных сумм не существует, ряд называется расходящимся.

Пример 1: Найти сумму ряда геометрической прогрессии.

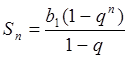Сумма первых  членов геометрической прогрессии со знаменателем  задается формулой (1): . Поскольку последовательность  при  и расходится при , имеем:

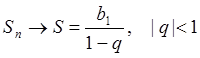,                                                       (54)

при  ряд расходится.

Например, 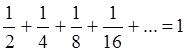 поскольку .

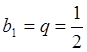Теорема 1 (необходимое условие сходимости ряда): Ряд  сходится    .

Действительно, если , то в сколь угодно удаленном «хвосте» последовательности существуют  такие, что , тогда члены последовательности частичных сумм  при сколь угодно больших  будут (по крайней мере иногда) получать конечное приращение  и выходить из - окрестности  предполагаемого предела  последовательности , что означает отсутствие предела у последовательности .   Ч.Т.Д.

Пример 2: Исследовать сходимость ряда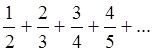

Поскольку , ряд расходится.

Отметим, что необходимое условие сходимости ряда не является достаточным, то есть стремление членов ряда к нулю не означает еще сходимость ряда. По сути дела мы сталкиваемся с неопределенностью . Действительно, если представить частичную сумму ряда  в виде произведения среднего арифметического значения первых  членов ряда  на число слагаемых , то .

Пример 3: Исследовать сходимость гармонического ряда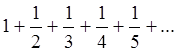

    

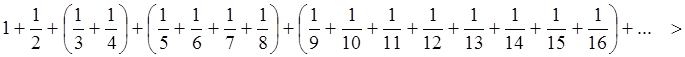
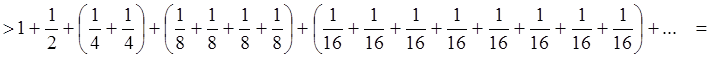
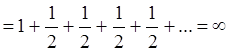
Ряд расходится, хотя .

Для оценки скорости возрастания частичной суммы гармонического ряда 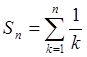 можно воспользоваться следующей формулой:

,                                                             (55)

где  есть иррациональное число (постоянная Эйлера).

Определение 3: Ряд, все члены которого одного знака называют знакопостоянным. Ряд, который содержит как положительные, так и отрицательные члены называют знакопеременным.

Поскольку сумма ряда с отрицательными членами отличается лишь общим знаком минус от суммы ряда с положительными членами, будем рассматривать знакоположительные ряды ().

Признаки сходимости знакоположительных рядов:

1)  Признак сравнения:

1.1  Пусть  или 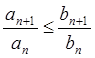, тогда             если сходится сходится,

если расходится расходится.

1.2 Пусть 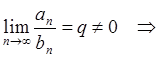    и  сходятся или расходятся одновременно.

2)  Признак Даламбера:

Пусть 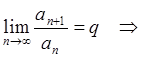   при  ряд сходится, при  ряд расходится.

3)  Признак Коши:

Пусть    при  ряд сходится, при  ряд расходится.

При  ряды могут оказаться как сходящимися, так и расходящимися.

Отметим, что сходимость или расходимость ряда не зависит от значений произвольного числа первых  членов ряда (сходимость определяется «хвостом» ряда), поэтому достаточно, чтобы вышеперечисленные условия выполнялись при всех , где  - некоторое натуральное число.

4)  Интегральный признак Коши:

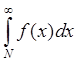Пусть  есть невозрастающая (убывающая) непрерывная функция при , тогда ряд  и интеграл  сходятся или расходятся одновременно.

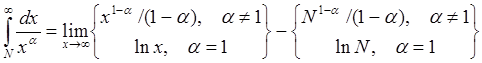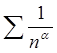В частности, интеграл  сходится при  и расходится при , соответственно ряд  сходится при  и расходится при .