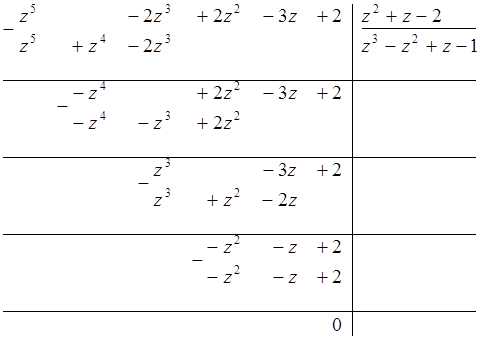
Математический анализ функции одной переменной: Учебное пособие. Часть 1 (Элементы математической логики. Множества чисел. Комплексные числа. Производная функции. Дифференциал), страница 5

Таким образом, .

Делителями свободного члена являются . Проверка показывает, что является корнем уравнения ( не является).

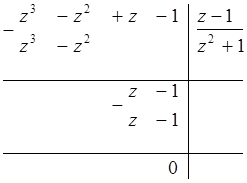
Окончательно получаем:

Таким образом, исходное алгебраическое уравнение имеет один двукратный корень и три простых корня .

6. Элементы комбинаторики

Определение 1: Упорядоченным подмножеством множества называют некоторую часть элементов из множества , расположенных в определенном порядке. Упорядоченные подмножества с одинаковым составом элементов, но различающиеся их порядком следования, считают различными (в отличие от обычных подмножеств).

Пример 1: Упорядоченными подмножествами множества являются: - пустое множество, - множества из одного элемента, - упорядоченные множества из двух элементов, - упорядоченные множества из трех элементов.

Определение 2: Пусть имеется множество , состоящее из элементов. Размещением из элементов по элементов называют любое упорядоченное подмножество множества , состоящее из элементов.

Определение 3: Числом размещений из по называют число различных упорядоченных - элементных подмножеств множества , состоящего из элементов.

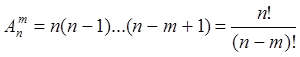(24)

Действительно, в качестве первого элемента можно взять любой из элементов множества , в качестве второго элемента – любой из оставшихся элементов, и т.д., наконец, в качестве последнего (- го) элемента – один из оставшихся элементов.

Пример 2: Найти число размещений .

Перебрав все упорядоченные двухэлементные подмножества множества , состоящего из трех элементов (пример 1), находим: . С другой стороны,

Определение 4: Перестановкой называют размещение из элементов по ().

Число различных перестановок определяется формулой:

(25)

Определение 5: Четностью (знаком) перестановки называют число где - число парных перестановок (только два некоторых элемента меняются местами), которые переводят тождественную перестановку в перестановку (или наоборот). После каждой парной перестановки четность перестановки меняется.

Пример 3: Определить четность перестановки .

Укажем последовательность парных перестановок, которая переводит исходную перестановку в тождественную: . Число парных перестановок (число стрелок) , следовательно, перестановка нечетная ().

Определение 6: Сочетанием из элементов по элементов называют любое обычное (неупорядоченное) - элементное подмножество множества , состоящего из элементов.

Определение 7: Числом сочетаний из по называют число различных (неупорядоченных) - элементных подмножеств множества , состоящего из элементов.

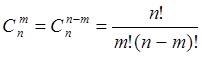(26)

Действительно, поскольку каждому сочетанию из элементов соответствует различных перестановок этих элементов, мы имеем .

Кроме того, .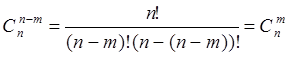

Пример 4: Найти число сочетаний .

Перебрав все двухэлементные подмножества множества , состоящего из трех элементов (пример 1: ), находим: . С другой стороны,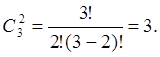

Используя понятие числа сочетаний можно легко получить формулу разложения для любой натуральной степени бинома (двучлена) . Действительно, при перемножении

слагаемое может быть получено следующими способами: в произвольных скобках из возможных мы выбираем в качестве множителя , в остальных – мы выбираем . Таким образом, число раз, которое встречается слагаемое в разложении бинома равно числу способов выбора некоторых скобок из возможных, то есть . В итоге, формула разложения для натуральной степени бинома