Пример 3: Исследовать существование предела функции ![]() при
при ![]() .
.
Для любого числа ![]() можно указать
можно указать ![]() , такое, что при всех
, такое, что при всех ![]() выполняется неравенство
выполняется неравенство ![]() , следовательно, согласно определению 3,
, следовательно, согласно определению 3, ![]() . Отметим, что график функции
. Отметим, что график функции ![]() (рис. 8) по мере удаления вправо пересекает
любую, сколь угодно высоко расположенную, горизонтальную линию
(рис. 8) по мере удаления вправо пересекает
любую, сколь угодно высоко расположенную, горизонтальную линию ![]() , что позволяет прийти к тому же
заключению.
, что позволяет прийти к тому же
заключению.
Все теоремы и свойства, приведенные в параграфе
10, могут быть непосредственно использованы для нахождения предела функции ![]() при
при ![]() .
.
Пример 4: Найти предел функции ![]() при
при ![]() .
.
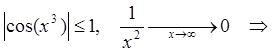 согласно Т2 из параграфа 10
имеем
согласно Т2 из параграфа 10
имеем 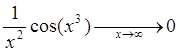 .
.
Пример 5: Найти предел функции 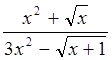 при
при ![]() .
.
Согласно утверждению 2 параграфа 10 имеем: 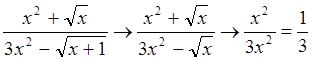 .
.
Как показано в предыдущем примере, при вычислении
предела функции мы пренебрегаем величинами, имеющими более высокий порядок
малости (малыми) по сравнению с величинами более низкого порядка малости
(большими). Иначе говоря, в сумме ![]() мы оставляем слагаемое
мы оставляем слагаемое
![]() , если
, если 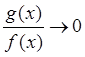 , или
наоборот, слагаемое
, или
наоборот, слагаемое ![]() , если
, если 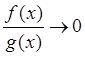 .
Приведем более точную классификацию малости одной величины по сравнению с
другой.
.
Приведем более точную классификацию малости одной величины по сравнению с
другой.
1)
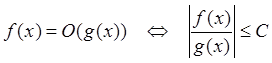 при
при ![]() .
.
Говорят, что ![]() является
величиной порядка малости не меньшего, чем
является
величиной порядка малости не меньшего, чем ![]() при
при ![]() , если отношение
, если отношение ![]() ограничено
для всех
ограничено
для всех ![]() , больших некоторого
, больших некоторого ![]() .
.
Отметим, что отношение ![]() не обязано иметь предел при
не обязано иметь предел при ![]() . Например,
. Например,
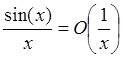 поскольку
поскольку 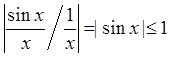 , однако
, однако 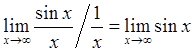 не
существует.
не
существует.
Перейдем к рассмотрению более частных случаев,
когда ![]() существует.
существует.
2)
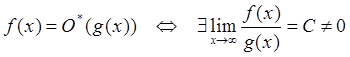
Говорят, что ![]() имеет
тот же порядок малости, что и
имеет
тот же порядок малости, что и ![]() если отношение
если отношение ![]() стремится к конечному, отличному от нуля
числу.
стремится к конечному, отличному от нуля
числу.
3)
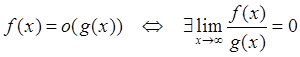
Говорят, что ![]() является
величиной более высокого порядка малости по сравнению с
является
величиной более высокого порядка малости по сравнению с ![]() , если отношение
, если отношение ![]() стремится
к нулю.
стремится
к нулю.
4)
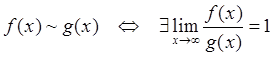 .
.
Говорят, что величины ![]() и
и ![]() эквивалентны
если отношение
эквивалентны
если отношение ![]() стремится к единице.
стремится к единице.
Утверждение 1: Пусть ![]() , тогда если
, тогда если ![]() , где
, где ![]() -
произвольная функция, то и
-
произвольная функция, то и ![]() .
.
Действительно, 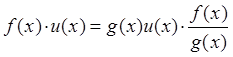 , функция
, функция ![]() ,
функция
,
функция ![]() ограничена, следовательно
ограничена, следовательно ![]() .
.
Утверждение 2: При вычислении предела функции в суммах можно пренебрегать величинами более высокого порядка малости по сравнению с величинами более низкого порядка.
Действительно, пусть ![]() , тогда
, тогда
![]() .
.
Утверждение 3: При вычислении предела функции можно заменять величину на эквивалентную.
Действительно, пусть ![]() , тогда
, тогда ![]() .
.
Утверждение 4: При вычислении предела функции нельзя пренебрегать одной величиной по сравнению с другой, имеющей тот же или больший порядок малости.
Для нахождения пределов функций необходимо
изначально классифицировать элементарные функции по порядку малости. Начнем с
классификации при ![]() . Нам уже известна классификация
степенных функций.
. Нам уже известна классификация
степенных функций.
Утверждение 5: При ![]() степенные функции с меньшим
показателем степени имеют более высокий порядок малости (следует оставлять
функции с большим показателем степени).
степенные функции с меньшим
показателем степени имеют более высокий порядок малости (следует оставлять
функции с большим показателем степени).
Утверждение 6: При ![]() показательные функции с меньшим
основанием имеют более высокий порядок малости (следует оставлять функции с
большим основанием).
показательные функции с меньшим
основанием имеют более высокий порядок малости (следует оставлять функции с
большим основанием).
Действительно, пусть ![]() , тогда
, тогда ![]() и
и ![]() (см.
рис. 7), откуда получаем
(см.
рис. 7), откуда получаем
![]() .
.
Утверждение 7: При всех ![]() , в частности, при
, в частности, при ![]() все логарифмические функции имеют
одинаковый порядок малости.
все логарифмические функции имеют
одинаковый порядок малости.
Действительно, 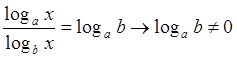 .
.
Сравним теперь различные классы элементарных функций между собой.
Утверждение 8: При ![]() степенные функции имеют более
высокий порядок малости, чем показательные функции с основанием, большим
единицы, и более низкий порядок малости, чем показательные функции с
основанием, меньшим единицы.
степенные функции имеют более
высокий порядок малости, чем показательные функции с основанием, большим
единицы, и более низкий порядок малости, чем показательные функции с
основанием, меньшим единицы.
Рассмотрим для начала 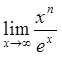 , где
, где ![]() - произвольное натуральное число.
- произвольное натуральное число.
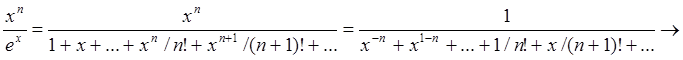
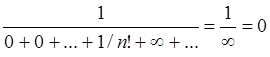 .
.
Поскольку для любой степенной функции ![]() можно
указать степенную функцию с большим натуральным показателем степени
можно
указать степенную функцию с большим натуральным показателем степени ![]() , которая растет быстрее, чем
, которая растет быстрее, чем ![]() , но медленнее, чем
, но медленнее, чем ![]() ,
получаем, что
,
получаем, что 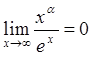 при любом
при любом ![]() . Рассмотрим теперь
. Рассмотрим теперь 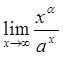 ,
где
,
где ![]() .
.
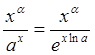 . Введя обозначение
. Введя обозначение ![]() , имеем
, имеем 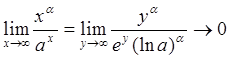 .
Первая часть утверждения 8 доказана.
.
Первая часть утверждения 8 доказана.
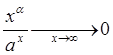 при любом
при любом ![]() и
и ![]() (62)
(62)
Перейдем к рассмотрению случая, когда ![]() .
Вводя обозначение
.
Вводя обозначение ![]() , имеем
, имеем
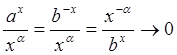 . Вторая часть утверждения 8
доказана.
. Вторая часть утверждения 8
доказана.
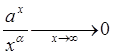 при любом
при любом ![]() и
и ![]() (63)
(63)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.