Примеры: ![]()
![]()
![]()
При рассмотрении расходящихся последовательностей также можно выделить три основных типа (см. рис. 15):
1)
Неограниченно
возрастающая последовательность ![]() . Отметим, что неограниченно
возрастающая последовательность не обязана быть монотонной. Важно, чтобы нижняя
граница «хвоста» последовательности
. Отметим, что неограниченно
возрастающая последовательность не обязана быть монотонной. Важно, чтобы нижняя
граница «хвоста» последовательности ![]() неограниченно
возрастала с ростом
неограниченно
возрастала с ростом ![]() :
: ![]() .
.
Примеры: ![]()
![]()
![]() .
.
Пример 6: Доказать, что ![]() .
.
![]()
![]()
2)
Неограниченно
убывающая последовательность ![]() . Для неограниченно
убывающей последовательности существенно, чтобы верхняя граница «хвоста» последовательности
. Для неограниченно
убывающей последовательности существенно, чтобы верхняя граница «хвоста» последовательности
![]() неограниченно убывала с ростом
неограниченно убывала с ростом ![]() :
: ![]() .
.
Примеры: 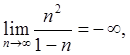
![]()
![]() .
.
Пример 7: Доказать, что ![]() .
.
![]()
Отметим, что оценка ![]() верна
для
верна
для ![]() и неверна для
и неверна для ![]() , однако
при вычислении пределов последовательностей важно, чтобы оценки выполнялись для
«хвоста» последовательности (начиная с некоторого произвольного
, однако
при вычислении пределов последовательностей важно, чтобы оценки выполнялись для
«хвоста» последовательности (начиная с некоторого произвольного ![]() ).
).
3) Последовательность, не имеющая предела (в том числе и бесконечного). Данная последовательность не является монотонной, причем амплитуда колебаний ее не стремится к нулю. Последовательность может быть как ограниченной, так и не ограниченной (с возрастающей амплитудой).
Примеры последовательностей, конечные и бесконечные пределы которых не существуют:
![]() - ограниченные
последовательности,
- ограниченные
последовательности,
![]() - неограниченные
последовательности.
- неограниченные
последовательности.
Пример 8*: Показать, что последовательность ![]() не
ограничена.
не
ограничена.
![]() неограниченно возрастает
(убывает) когда
неограниченно возрастает
(убывает) когда ![]() приближается к значениям
приближается к значениям ![]() справа (слева), см. рис. 11. Таким
образом, последовательность не ограничена, если
справа (слева), см. рис. 11. Таким
образом, последовательность не ограничена, если ![]() периодически
(при больших
периодически
(при больших ![]() ) принимает значения, сколь угодно близкие
к
) принимает значения, сколь угодно близкие
к ![]() . Поскольку иррациональное число
. Поскольку иррациональное число ![]() может быть с любой степенью точности
аппроксимировано рациональным числом
может быть с любой степенью точности
аппроксимировано рациональным числом 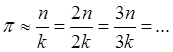 , в сколь угодно
далеком «хвосте» последовательности найдется число
, в сколь угодно
далеком «хвосте» последовательности найдется число ![]() , такое
что
, такое
что ![]() больше любого наперед заданного числа.
Ч.Т.П.
больше любого наперед заданного числа.
Ч.Т.П.
Основные свойства пределов последовательностей:
Пусть ![]()
1) ![]()
2) ![]()
3) 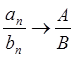
4) ![]()
Все перечисленные свойства легко доказываются на основе общего определения 2.
Если ![]() есть непрерывная функция своих
аргументов (см. §13), то
есть непрерывная функция своих
аргументов (см. §13), то
5)
![]()
6)
![]()
Пример 9: Найти предел последовательности 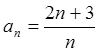 .
.
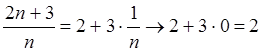
Пример 10: Найти предел последовательности 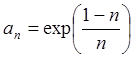 .
.
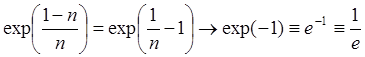
Пример 11: Найти предел последовательности 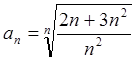 .
.
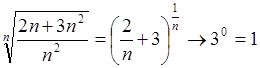
Утверждение 1: 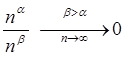 .
.
Действительно, ![]() (см. рис. 4). Строгое
доказательство утверждения
(см. рис. 4). Строгое
доказательство утверждения ![]() полностью аналогично
доказательству из примера 2.
полностью аналогично
доказательству из примера 2.
Утверждение 2: При вычислении пределов последовательностей в сумме ![]() следует оставлять только слагаемое с
большим показателем степени:
следует оставлять только слагаемое с
большим показателем степени: ![]() .
.
Действительно, 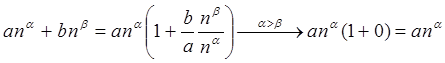 .
.
Пример 12: Найти предел последовательности 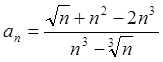 .
.
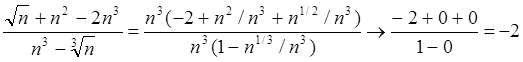
Иначе: 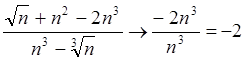
Определение 5: Говорят, что последовательность ![]() стремится к нулю справа (слева),
если
стремится к нулю справа (слева),
если ![]() и, начиная с некоторого
и, начиная с некоторого ![]() , все члены последовательности
, все члены последовательности ![]()
![]() . Пишут
. Пишут ![]() .
.
Отметим, что свойства 1-6 пределов
последовательностей можно формально использовать и в случае, когда ![]() и/или
и/или ![]()
![]() . В этом случае необходимо учесть следующие
формальные правила символьных вычислений:
. В этом случае необходимо учесть следующие
формальные правила символьных вычислений:
Пусть ![]() есть некое постоянное
(не зависящее от
есть некое постоянное
(не зависящее от ![]() ) положительное число, тогда
) положительное число, тогда
![]() (49)
(49)
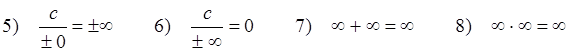
Пример 13: Найти предел последовательности ![]() .
.
![]()
Пример 14: Найти предел последовательности ![]() .
.
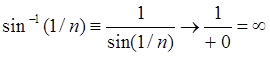
Следует отметить, что независимое вычисление
пределов последовательностей ![]() ,
, ![]() с последующей попыткой определить предел
последовательности
с последующей попыткой определить предел
последовательности ![]() как
как ![]() не
всегда приводит к однозначному результату. В ряде случаев возникают соотношения
символов, которые не позволяют определить предел
не
всегда приводит к однозначному результату. В ряде случаев возникают соотношения
символов, которые не позволяют определить предел ![]() . Такие
соотношения носят название соотношений неопределенности. Появление соотношения
неопределенности свидетельствует о том, что пределы последовательностей
. Такие
соотношения носят название соотношений неопределенности. Появление соотношения
неопределенности свидетельствует о том, что пределы последовательностей ![]() и
и ![]() нельзя
рассматривать по отдельности. В этом случае следует вычислять предел
последовательности
нельзя
рассматривать по отдельности. В этом случае следует вычислять предел
последовательности ![]() непосредственно, без
использования символьных обозначений.
непосредственно, без
использования символьных обозначений.
К наиболее часто встречающимся соотношениям неопределенности относят:
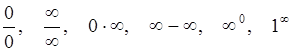 (50)
(50)
Пример 15: Найти пределы последовательностей 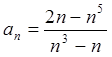 ,
, 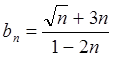 ,
, 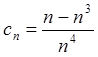 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.