Утверждение 9: При ![]() логарифмические функции имеют
более высокий порядок малости, чем степенные функции с показателем, большим
нуля.
логарифмические функции имеют
более высокий порядок малости, чем степенные функции с показателем, большим
нуля.
Действительно, вводя обозначение ![]() , получаем при
, получаем при ![]() :
: 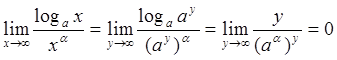 (смотри (62),
(смотри (62), ![]() ).
).
При ![]() , вводя обозначение
, вводя обозначение ![]() , имеем
, имеем
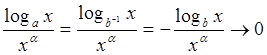 . Утверждение 9 доказано.
. Утверждение 9 доказано.
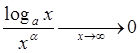 при любом
при любом ![]() и
и ![]() (64)
(64)
Утверждение 10: При ![]() показательные функции
показательные функции ![]() имеют более высокий порядок малости, чем
функция
имеют более высокий порядок малости, чем
функция ![]() .
.
При ![]() , когда
, когда ![]() , утверждение очевидно. Покажем, что при
, утверждение очевидно. Покажем, что при ![]() , когда
, когда ![]() , имеет
место аналогичный предел
, имеет
место аналогичный предел 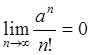 . Выберем натуральное
число
. Выберем натуральное
число ![]() такое, что
такое, что ![]() , тогда
, тогда
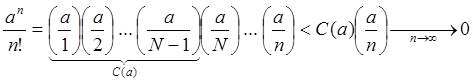 . Утверждение 10 доказано.
. Утверждение 10 доказано.
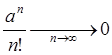 при любом
при любом ![]() (65)
(65)
Для удобства
дальнейшего использования суммируем полученные результаты, расположив основные элементарные
функции в порядке увеличения их скорости возрастания при ![]() .
.
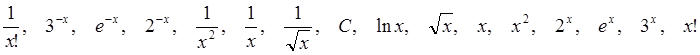 (66)
(66)
Здесь ![]() включает в себя класс
ограниченных, отделенных от нуля функций, которые при больших
включает в себя класс
ограниченных, отделенных от нуля функций, которые при больших ![]() удовлетворяют условию
удовлетворяют условию ![]() . Все функции, расположенные справа от
. Все функции, расположенные справа от ![]() стремятся к
стремятся к ![]() при
при ![]() , все функции, расположенные слева от
, все функции, расположенные слева от ![]() , стремятся к
, стремятся к ![]() при
при ![]() . Если
. Если ![]() есть
произвольная функция, расположенная правее некоторой другой функции
есть
произвольная функция, расположенная правее некоторой другой функции ![]() , то выполняются следующие предельные
соотношения:
, то выполняются следующие предельные
соотношения:
![]() .
.
Пример 6: Найти предел функции 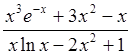 при
при ![]() .
.
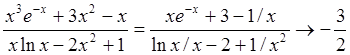 поскольку
поскольку ![]() ,
,
![]() .
.
Пример 7: Найти предел функции 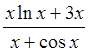 при
при ![]() .
.
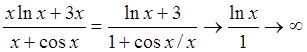 поскольку
поскольку 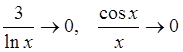 .
.
Пример 8: Найти предел функции ![]() при
при ![]() , где
, где ![]() - любое число.
- любое число.
Раскроем неопределенность ![]() ,
используя основное логарифмическое тождество, а также известный предел
,
используя основное логарифмическое тождество, а также известный предел ![]() . Получаем:
. Получаем: ![]() .
.
Перейдем к рассмотрению предела функции при
![]() . Определение предела функции при
. Определение предела функции при ![]() совпадает с определением 1, с точностью
до замены
совпадает с определением 1, с точностью
до замены ![]() на
на ![]() .
Действительно, теперь речь идет о больших по модулю отрицательных значениях
переменной
.
Действительно, теперь речь идет о больших по модулю отрицательных значениях
переменной ![]() , меньших любого заданного числа
, меньших любого заданного числа ![]() . С точки зрения построения графика,
наличие у функции
. С точки зрения построения графика,
наличие у функции ![]() при
при ![]() конечного
предела, равного
конечного
предела, равного ![]() , означает, что график функции
, означает, что график функции ![]() имеет в области больших по модулю
отрицательных
имеет в области больших по модулю
отрицательных ![]() (далеко слева) горизонтальную
асимптоту
(далеко слева) горизонтальную
асимптоту ![]() .
.
Дадим еще одно эквивалентное определение
предела функции при ![]() .
.
Определение 4:
![]() (67)
(67)
Данное определение позволяет свести рассмотрение предела
функции ![]() при
при ![]() к
рассмотрению предела другой функции
к
рассмотрению предела другой функции ![]() при
при ![]() . Новая функция
. Новая функция ![]() получается
из
получается
из ![]() путем повсеместной замены
путем повсеместной замены ![]() на
на ![]() в
выражении для
в
выражении для ![]() .
.
Пример 9: Найти предел функции ![]() при
при ![]() и при
и при ![]() .
.
Как видно из графика функции ![]() на
рис. 13, функция имеет горизонтальную асимптоту
на
рис. 13, функция имеет горизонтальную асимптоту ![]() в
области больших положительных
в
области больших положительных ![]() и горизонтальную
асимптоту
и горизонтальную
асимптоту ![]() в области больших отрицательных
в области больших отрицательных ![]() . Следовательно,
. Следовательно, ![]() .
.
Второй предел можно выразить
также через первый, использую определение 4 и свойство нечетности функции ![]() :
: ![]() .
.
Пример 10: Найти предел функции 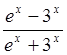 при
при ![]() и при
и при ![]() .
.
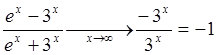 . Здесь мы пренебрегли
. Здесь мы пренебрегли ![]() по сравнению с
по сравнению с ![]() (см.
(66)).
(см.
(66)).
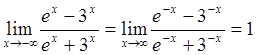 . Теперь мы пренебрегаем
. Теперь мы пренебрегаем ![]() по сравнению с
по сравнению с ![]() (см.
(66)).
(см.
(66)).
В целом, классификация
функций по порядку малости при ![]() выглядит аналогично
(66). Основное отличие составляют показательные функции, для которых порядок малости
возрастает теперь с ростом основания.
выглядит аналогично
(66). Основное отличие составляют показательные функции, для которых порядок малости
возрастает теперь с ростом основания.
13. Предел при ![]() .
Непрерывность функции. Классификация точек разрыва.
.
Непрерывность функции. Классификация точек разрыва.
Перейдем к рассмотрению предела функции при ![]() , где
, где ![]() есть
некое конечное число. Различают пределы при
есть
некое конечное число. Различают пределы при ![]() справа,
из области
справа,
из области ![]() , и слева, из области
, и слева, из области ![]() .
.
Определение 1: Говорят, что функция ![]() имеет
при
имеет
при ![]() справа (слева) предел, равный
справа (слева) предел, равный ![]()
![]() , если
для любого (сколь угодно малого)
, если
для любого (сколь угодно малого) ![]() можно указать
можно указать ![]() , такое что для всех
, такое что для всех ![]() выполняется неравенство
выполняется неравенство ![]() (
(![]() ).
Пишут
).
Пишут
![]() или
или ![]() . (68)
. (68)
Другое, эквивалентное определение позволяет выразить предел
функции при ![]() через предел при
через предел при ![]() .
.
Определение 2: Пусть ![]() (
(![]() при больших
при больших ![]() ), тогда
), тогда
![]() .
(69)
.
(69)
В частности, для случая ![]() ,
выбирая в качестве
,
выбирая в качестве ![]() функцию
функцию ![]() ,
получаем:
,
получаем:
![]() . (70)
. (70)
Определение 3: Если пределы функции при ![]() справа
и слева существуют и совпадают, то говорят, что функция непрерывна в точке
справа
и слева существуют и совпадают, то говорят, что функция непрерывна в точке ![]() . В этом случае
. В этом случае
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.