Предмет гидравлика и основные физические свойства жидкости. Основные физические свойства жидкости. Понятие об идеальной жидкости, страница 8

Если центр тяжести расположен ниже центра водоизмещения, то тело стремится возвратиться в прежнее положение – оно остойчиво (рис 1.28.).

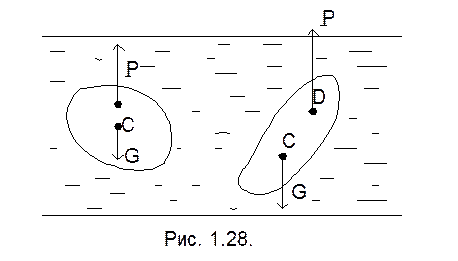
Если центр тяжести расположен выше центра водоизмещения, то тело, выведенное из состояния равновесия, не сможет возвратиться в первоначальное положение – оно не остойчиво (рис 1.29.).

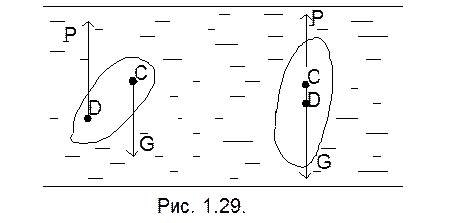
Если центр тяжести и центр водоизмещения совпадают, то имеет место безразличное состояние равновесия (рис 1.30.).

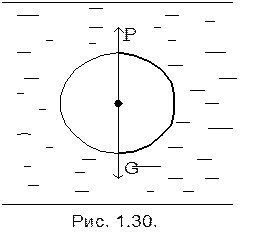
Задачи и примеры их решения в общем виде.

Задача 1. Определить давление газа в баллоне по показанию h   двух жидкостного чашечного микроманометра, заполненного жидкостями,   имеющими плотности ρ₁и,ρ₂если задано отношение диаметров трубки и чашки прибора D/d (рис. 1.31.).

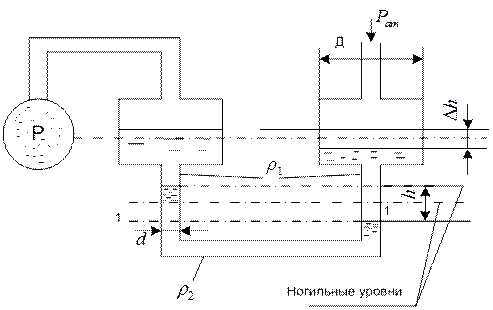
Рис. 1.31.

Для определения давления применим закон равновесия,  из которого следует,  что в жидкости плотностьюρ₂на уровне 1-1 давление в трубках манометра одинаково. В правой трубке оно создано атмосферным давлением р_ат и весовым давлением столба жидкости плотностью ρ₁. Так как высота этого столба неизвестна,   введем размерX.

Воспользовавшись выражением (10) получаем:

          р₁= р_ат + ρ₁ g (h + X).                                           (1-1)

В левой трубке давление на уровне 1-1 создается давлением газа р  и весовым давлением жидкостей,  имеющих плотности ρ₁ иρ₂ .

Для выражения давления введем еще размер ∆h, представляющий равность уровней жидкости плотностью  ρ_1.

Тогда получаем:

          р = ρ₁ g (X+ ∆h) + ρ₂ gh.                                          (1-2)

Приравняв соотношения (1-1) и (1-2) получаем:

р =ρ₁ g(X+ ∆h) + ρ₂ gh= р_ат+ ρ₁ g(h+ X) ,                      

откуда

р = р_ат – (ρ₂ - ρ₁) gh - ρ₁ g∆h.                             (1-3)

Как видно,   использование только закона равновесия недостаточно для решения задачи, так как величина ∆h неизвестна.

Для определения ∆h применим уравнение постоянства объема жидкости в системе:

∆h D ² =  h d ² ,                                                          (1-4)

откуда

∆h = h d ² / D ².

Подставив ∆h в уравнение (1-3), получим:

р = р_ат – (ρ₂ - ρ₁) gh - ρ₁ gh d ²/D ².                      (1-5)                

Из рисунка видно, что р < р_ат, т.е. в баллоне вакуум.

Тогда, используя выражение (14) можно записать:

р_вак = (ρ₂ - ρ₁) gh + ρ₁gh d ²/D ².                            (1-6)        

Если  d значительно <  D, можно принять:

р_вак = (ρ₂ - ρ₁) gh.                                           (1-7)

Задача 2. На рисунке 1.32. рассмотрим в виде примера определение силы давления с помощью суммарной эпюры в случае  двустороннего воздействия жидкостей одинаковой плотности ρ на стенку при различных высотах уровней Н₁  и Н₂  по обе стороны стенки и одинаковом давлении на свободных поверхностях   I  и II.

Рис. 1.32.

Для верхнего участка стенки ав,  подверженного одностороннему  давлению жидкости (эпюра нагрузки представляет в плоско- сти чертежа треугольник авс),  сила  давления Р₁ определяется по формуле (27) и для нашего случая имеет вид:                      

,                                                          (2-1)

где:   h_с1 -  расстояние центра тяжести С₁, верхнего участка стенки до свободной поверхности  I;

S₁ - площадь данного участка.

Координата h_g,  центра давления участка ав,вычисляется по формуле (28) и  для нашего случая имеет вид:

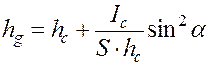                                                    (2-2)

Из рассмотрения эпюр давления на каждой стороне стенки (треугольники с основаниями ρgН₁  и ρgН₂ следует,   что разность давлений по обе стороны стенки на нижнем участке  вс   постоянна и равна pρgН (Н=Н₁ - Н₂  разность уровней жидкости); суммарная эпюра нагрузки для этого  участка вс gс.

Следовательно, сила давления на нижнем участке:

,                                                          (2-3)

где:    S₂ - площадь нижнего участка.

Сила Р₂ проходит через центр тяжести С₂ площади S₂. Результирующая сила Р = Р₁ + Р₂ , линия ее действия делит отрезок между точками D₁ и С₂  на части обратно пропорциональные силам Р₁ и Р₂.