Напишем уравнение Бернулли для сечений 1-1, 2-2.
.
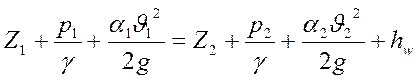При
больших резервуарах скорости 
и 
малы, а разность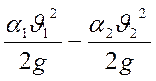 
близка
к 0.
Тогда для нашего случая в уравнении Бернулли получаем:
; pа=p1=p2; =; Н=hw=hwдл.
Следовательно, разность уровней Н, существующая между двумя резервуарами, полностью расходуется на преодоление сопротивлений в трубопроводе:
.
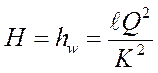Т.е. для простого трубопровода постоянного диаметра напор H можно считать по данной формуле (т.е. формуле (111) или (145)).
На рис. 1.84. представлена графическая характеристика простого трубопровода.
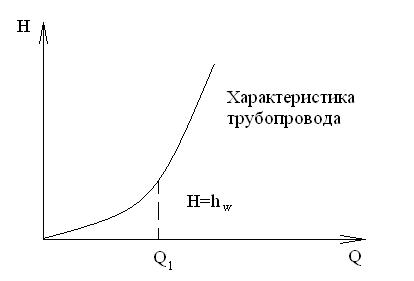
Рис. 1.84. Характеристики простого трубопровода.
2. Расчет простого трубопровода, переменного диаметра.
Если простой трубопровод состоит из труб разного диаметра (рис. 1.85.), то зная диаметр труб и их длины можно составить расходные характеристики для участников:
; 
; 
, где, hw1, hw1, hw1 – потери энергии на участках;
К1, К2, К3 – расходные характеристики;
d1, d2, d3 и ℓ1, ℓ2, ℓ3 – размеры труб.
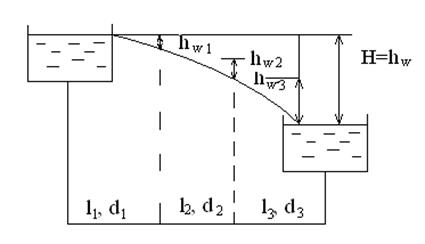
Рис. 1.85. Простой трубопровод переменного диаметра.
Тогда общие потери энергии в трубопроводе Hw равны сумме потерь на участках:
;
;
или в общем виде:
. (146)
Таким образом, при транзитном расходе через последовательно соединенные трубы необходимый напор равен произведению квадрата расхода на сумму удельных сопротивлений всех участников.
Для построения пьезометрических линий вычислим значения hw1, hw2, hw3 и, отложив в масштабе на чертеже, получим ломаную линию, состоящую из отдельных прямолинейных участников.
В практике приходится решать следующие задачи:
1. Определение расхода Qв трубопроводе при известных: длине – ℓ, диаметре – d и потерях напора – hw=H.
2. Определение потери напора hw в трубопроводе при известных: длине – ℓ, диаметре – d, расходе – Q.
3. Определение потребного диаметра – dтрубопровода при известных: длине – ℓ, расходе – Q, потерях напора – hw=H.
Характеристики последовательного соединения труб представлены на рисунке 1. 86.
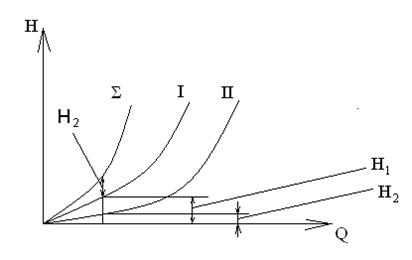
Рис. 1. 86. Характеристика трубопровода переменного диаметра.
1.3.14.2. Гидравлический расчет сложных трубопроводов
1. Расчет трубопровода с параллельным соединением линий.
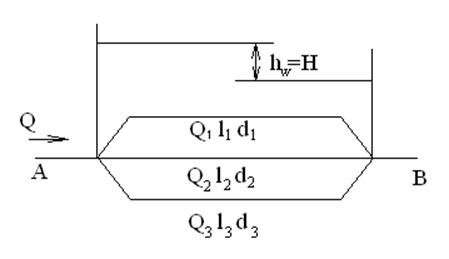
Рис. 1. 87. Схема сложного трубопровода с параллельным подключением.
Из пункта А в пункт В подается жидкость в количестве Q, л/сек. В точке А трубопровод разветвляется на 3 линии.
Расход Q можно определить по формуле:
, (147)
где, 
, 
, 
.
Так как пьезометрическое давление в точках А и В одинаково для всех линий, поэтому и потери напора для всех участков одинаковы:
, где, 
, , .
Тогда:
, или
. (148)
Определив расход, можно определить и потери в параллельной сети:
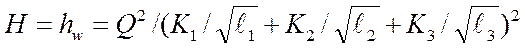. (149)
Из уравнения (149) следует, что потери напора при параллельном подключении сети уменьшаются на количество линий трубопровода.
На рисунке 1. 88. представлена характеристика трубопровода с параллельным соединением труб.
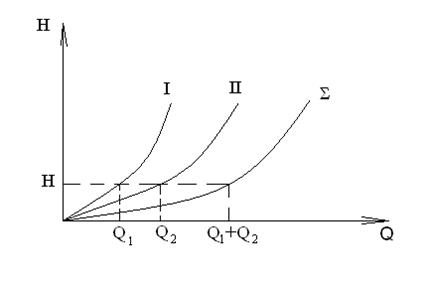
Рис. 1. 88. Характеристика параллельного соединения труб.
2. Расчет трубопровода с непрерывным расходом по его длине.
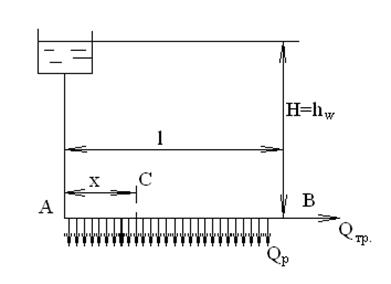
Рис. 1. 89. Схема трубопровода с распределяемым расходом по длине.
Рассмотрим сечение С на расстоянии х от начала участка, в котором расход можно определить по формуле:
, (150)
где, 
- транзитный расход,
-
путевой расход,
-
расход на участке,
- удельный
расход (удельный путевой расход).
Удельным расходом q - количество жидкости, отводящееся через отверстие с каждой единицы длины трубопровода.
Возле точки С возьмем отрезок бесконечно малой длины dx и напишем уравнение падения напора:
.
Проинтегрируем данное уравнение в пределах от 0 до ℓ и принимая ориентировочно, что K=const, получаем:
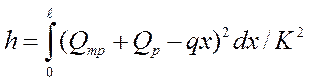
После интегрирования и преобразований получаем:
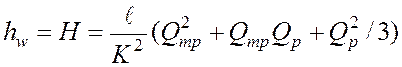. (151)
Если транзитный расход равен нулю (
), то получаем:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.