Предмет гидравлика и основные физические свойства жидкости. Основные физические свойства жидкости. Понятие об идеальной жидкости, страница 16

Закон распределения скоростей по сечению круглой трубы при ламинарном движении.

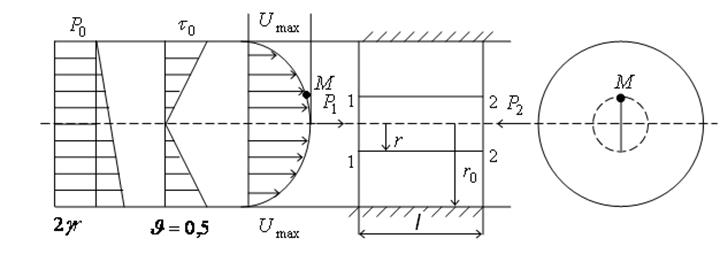
Рис. 1.55.   Закон распределения скоростей по сечению круглой трубы. 

Скорость движения каждого слоя жидкости при ламинарном режиме  движения можно определить по формуле:

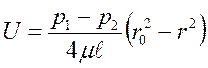.                                                               (80)

По параболическому закону распределения скоростей при ламинарном движении (закон Стокса) можно определить максимальную скорость  при условии, что :

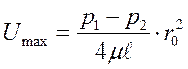.                                                                  (81)

Тогда, после подстановки, выражение (1.79.) приобретает вид:

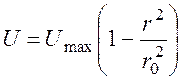.                                                                   (82)

Но т.к.:

, то  касательное напряжение в поперечном сечении трубы , можно определить по формуле:

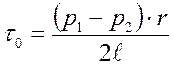.                                                                              (83)

Для распределения скоростей по длине потока (рис. 1.56.), различными авторами, установлены следующие соотношения:

Буссинеску, при 99%:

.                                                                          (84)

Шиллер, при 85% :

,                                                                          (85)   

где:     - начальный участок.

Т.е., при ,  - так называемый калибр.

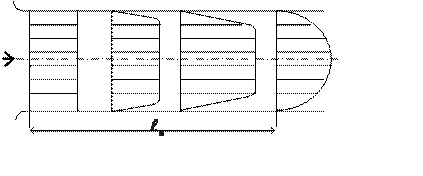
Рис. 1.56.  Схема скоростей на входе в трубопровод.

Расход при ламинарном движении в трубе.

Для определения средней скорости движения жидкости, определим расход Q через трубу, равный сумме элементарных расходов через кольца радиусом  и шириной  (рис. 1.57.):

;

но ;

воспользовавшись выражением (79) получаем:

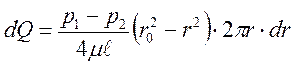; тогда:

.

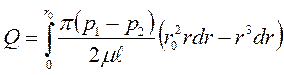После интегрирования получаем формулу для определения расхода:

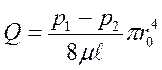.                                                                      (86)                                      

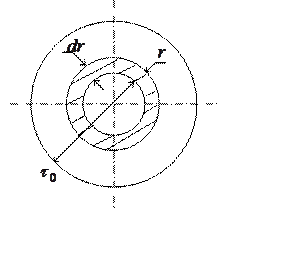
Рис. 1.57.    К определению расхода.

Если расход выразить через расходQ через среднюю скорость , то получаем:

.                                                                             (87)

Воспользовавшись выражением (86) получаем:

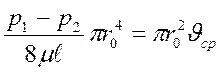       , откуда:

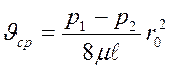.                                                                               (88)

Сравнив выражения (81)  и (88) окончательно получаем:

.                                                                          (89)

Т.е. средняя скорость в ламинарном потоке жидкости в круглой трубе равна половине максимальной скорости этого потока.

Потери напора при ламинарном движении.

Для определения потерь напора воспользуемся рисунком 1.58. и уже известными нам выражениями.

Рис. 1.58.  Потери напора.

В соответствии с рисунком 1.58. получаем:

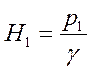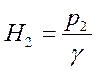; ;     тогда ;

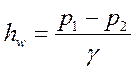но, ;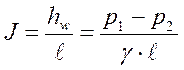

а, 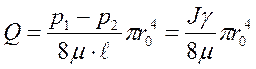;     воспользовавшись; ; ;

получаем: 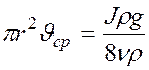; или ;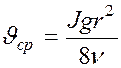

то есть 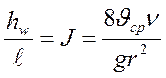; но 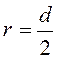, тогда:

;

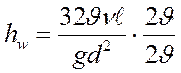подставив число Рейнольдса (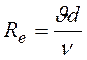) окончательно получаем формулу Пуазейля для определения потерь напора при ламинарном движении в круглых трубах:

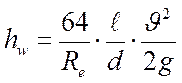.                                                                   (90)

Если  ввести понятие - коэффициент сопротивления трения по длине λ (коэффициент Дарси):

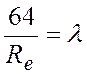.                                                                                   (91)

То получаем универсальная формулу Дарси, для определения потери энергии (напора) по длине (первая водопроводная формула).

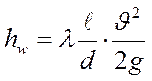^.                                                                        (92)

Для определения потерь напора начального участка Френкель ввел поправочный коэффициент К и его можно определить по графику (рис. 1.59.).

     

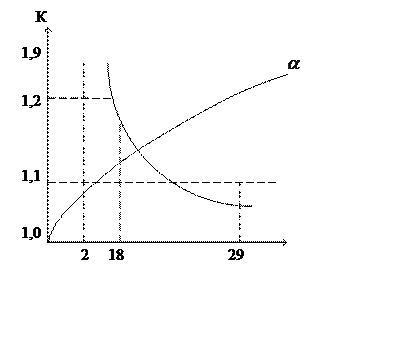
К                                                                        ;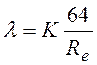

                      

 

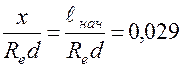
Рис. 1.59. Определение поправочного коэффициента.

Установлено, что сопротивление начального участка на 9% больше, чем при установившемся  ламинарном движении и его можно определить по формуле:                                    

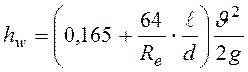.                                                        (93)

Опытами установлена зависимость коэффициента сопротивления трения по длине трубы λ, в зависимости от формы трубы: