Предмет гидравлика и основные физические свойства жидкости. Основные физические свойства жидкости. Понятие об идеальной жидкости, страница 23

Исходя из практики, для насадок  рекомендована следующая зависимость;

,                                                              (133)

где,     - угол наклона, градус;

 - диаметр, м;

 - напор, м.

Применима при углах от  до .

Опыты показывают, что если струя вытекает из насадки (брандспойта) и ее наклоняем, то ее компактная часть описывает траекторию.

Наибольшая дальность боя при углах  для м, при  для м.

Теоретически максимальная дальность имеет место при .

Дальность полета дождевальных струй определяется по формуле:

.                                                                   (134)

Получить хороший распыл при большей дальности удается при угле .

Формула применима при .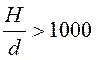

Динамические свойства струи.

Рассмотрим динамическое воздействие струи (удар) о неподвижную стенку, находящуюся на расстоянии, меньше длины компактной струи (рис. 1.80.).

Струя имеет цилиндрическую форму с осью NN – ось удара. Передача давления на тело происходит на участке растекания.

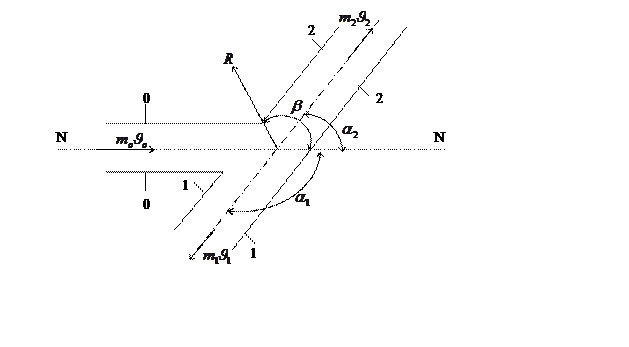
Рис. 1.80.  Взаимодействие струи с наклонной преградой.

Обозначим количество движения секундной массы жидкости . В сечениях 0-0, 1-1, 2-2 через , ,  (под секундной массой подразумевается масса = расходу ).

,  - направление векторов количеств движения.

Неподвижная поверхность, заставляя струю отклоняться, действует на нее с некоторой силой R (под углом ) .

Для определения величины и направления силы R воспользуемся теоремой об изменении количества движения в проекциях на ось N-N  и на ось к ней перпендикулярную (пренебрегая весом), что равно проекции импульса силы за то же время.

;

Считая , имеем 3 неизвестных , , .

Рассмотрим случай симметричного удара (простой). Направление  совпадает с осью N-N (рис. 1.81.),   тогда получаем:

;

;

; ;

Но  - статическое давление от напора  на площадку , откуда следует, что активное давление в 2 раза больше статического.

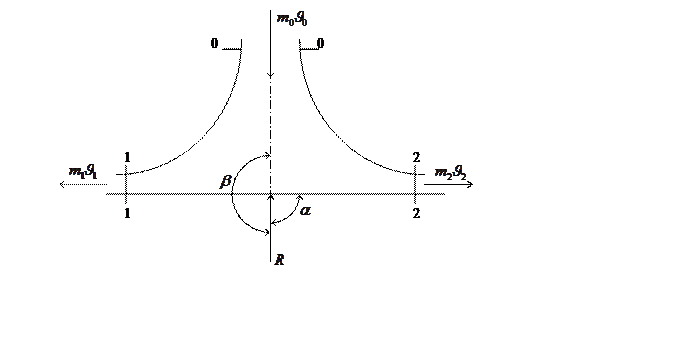
Рис. 1.81.  Взаимодействие струи с плоской стенкой.

Т.е. сила реакции пластинки равна по величине количеству движения, набегающей секундной массы жидкости:

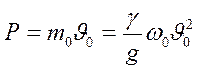,                                                                 (135)

где,  - живое сечение набегающей струи.

Действительное значение силы равно:

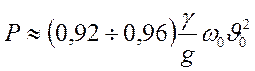.                                                       (136)

Силу удара можно повысить, если создать стенку, при которой  станет отрицательным (рис.1.82.).

Если 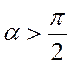, то  , тогда, или:

.                                                             (137)

При () получаем максимальное давление, тогда:

,

Или используя выражение , получаем:

.                                                           (138)

Рис.1.82.   Взаимодействие струи с криволинейной стенкой.

При движении лопатки со скоростью U вдоль струи, относительная скорость струи , тогда после подстановки получим:

, используя выражение получаем:

                                                           (139)

Обычно по этому типу выполняют лопатки турбин.

При движении лопатки максимальная работа будет получена при скорости равной скорости набегающего потока.

С помощью колеса с плоскими лопатками максимально можно использовать только половину кинетической энергии потока, поступающего на лопатки, тогда максимальная мощность:

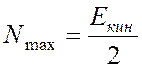,                                                                          (140)  

где,  - кинетическая энергия секундного расхода.

Мощность можно определить:

 

Если же угол , как это делают в турбинах, то сила давления станет вдвое больше, чем при плоских лопатках, а максимальная мощность будет равна кинетической энергии секундного расхода:

.                                                                          (141)

Т.е. реактивная энергия в два раза больше силы гидравлического давления.

1.3.14. Гидравлический расчет трубопроводов

Рассмотрим движение жидкости в трубопроводах, работающих полным сечением и под постоянным напором (напорное, установившееся движение).

Тогда средняя скорость определяется формулой Шези (103):