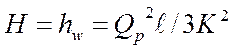Предмет гидравлика и основные физические свойства жидкости. Основные физические свойства жидкости. Понятие об идеальной жидкости, страница 26

.                                                           (152)

Из выражения (152) можно сделать следующий вывод: при непрерывной раздаче потери напора в три раза меньше, чем при транзитной подаче такого же расхода.

Учитывая, что: 

, введем понятие расчетного расхода Q_расч:

,                                                          (153)

получим формулу для практического пользования, пригодна для транзитного, непрерывного и смешанного расхода.

.                                                                   (154)

1.3.14.3.  Расчет гидравлических коротких трубопроводов

В гидравлически коротких трубопроводах основными потерями напора являются местные потери (рис. 1. 90.).

При гидравлическом расчете коротких трубопроводов решаются следующие задачи:

1.       Определение потерь напора h_w при известных типах местных сопротивлений и расходе Q.

2.       Определение расхода трубопроводов Q.

Известны диаметр и потери напора.

3.       Определение потребного диаметра трубопровода d для пропуска заданного расхода Q при известных потерях напора h_w.

Первые две задачи решаются по формулам, получаемым подстановкой в выражение (114) , выражений (92) и (117):          

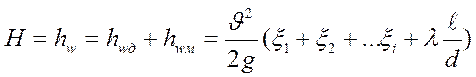, или:

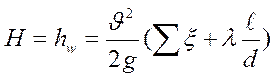,                                                    (155)

где,  - суммарные местные потери в трубопроводе.

Введя понятие потери в системе ξ_с :

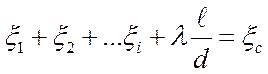
и используя известные выражения для определения средней скорости:

, получаем:

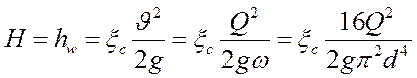.                            (156)

Расход в этом случае можно определить по формуле:

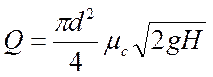,                                                              (157)

где: -  коэффициент расхода системы.

Третья задача (пренебрегая потерями по длине) решается по формуле, полученной из выражения (156):

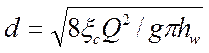.                                                               (158)

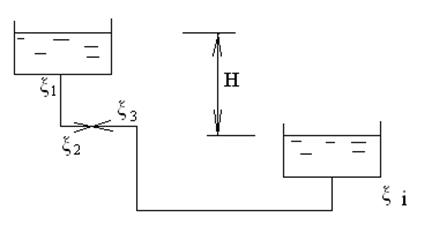
Рис. 1. 90. Схема короткого трубопровода.

Расчет всасывающей трубы насоса.

Всасывающий трубопровод характеризуется наличием вакуума, наибольшего у входа в насос (перед колесом) рисунок 1. 91.

Решая уравнение Бернулли

,

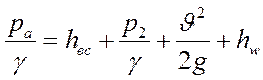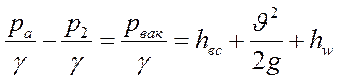, получаем:

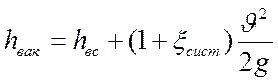,                                                   (159)

где, h_вак – вакуум перед рабочим колесом насоса.

Обычно h_вак  6,5 м. вод. ст.

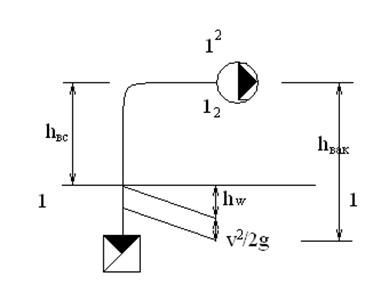
Рис. 1. 91. Схема расчета всасывающей трубы.

Допустимый вакуум зависит от температуры жидкости, так при температуре воды t= 60 ˚С, р_{вак.доп.} приобретает отрицательное значение – насос устанавливают ниже уровня жидкости:

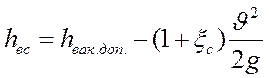
Расчет сифона.

Сифон – это трубопровод, часть которого располагается выше уровня жидкости верхнего резервуара, и по которому жидкость движется самотеком из питающего резервуара в приемный (рис. 1. 92.).

Работа сифона основана на действии вакуума, создающегося в самой высокой точке сифона (сечение 2-2). Для работы сифона его необходимо заполнить водой или создать вакуум при помощи вакуум-насосов.

Расчет сифона заключается в определении его пропускной способности и предельного значения высоты сифона h, при которой он может работать.

Расчет пропускной способности Q сифона производится по формуле (157):                                           

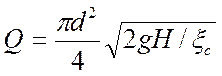, или , где:    - коэффициент расхода системы,

Н - разность уровней жидкости.

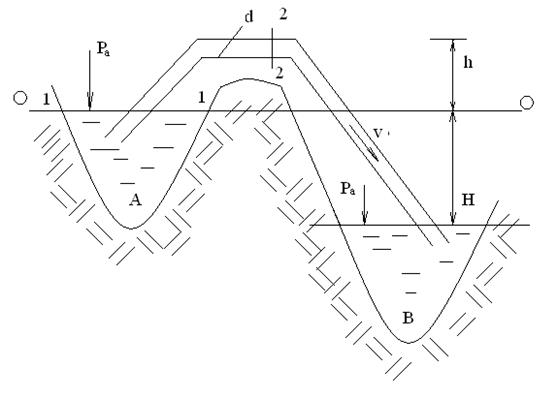
Рис. 1. 92.  Схема расчета сифона.

Расчет высоты сифона.    

Напишем уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0.

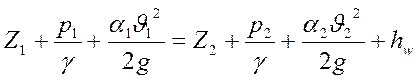, где,    р₂ – гидростатическое давление в сечении 2-2, при этом из рисунка 1. 92.  получаем:Z₁=0, Z₂=h, р₁=р_а; v₁=0; α₁=α₂=1.

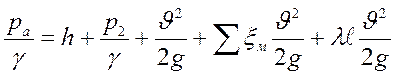
где,     - сумма коэффициентов местных потерь,

h– высота подъема,

υ – скорость в трубе.

Так как , то 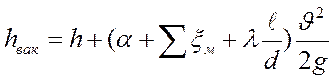     , откуда получаем:

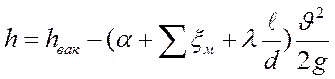.                                          (160)

Так как предельное значение вакуума 10,0 метров водного столба, то учитывая наличие потерь энергии в сифоне, а также невозможность большого понижения давления в нем и во избежание кавитации, высоту подъема обычно принимают не более 7-8 м. водн. ст.

1.3.14.4. Расчет сложных разветвленных трубопроводов

Различают два вида сложных трубопроводов:

1. Тупиковый, разветвленный (рис. 1. 93.).