Несмотря на относительную незначительность запасов грунтовых вод, роль их в природе и в жизни человека весьма велика. Режим грунтовых вод в поверхностных слоях земли во многом определяет условия развития растительности и, следовательно, возможный характер сельского хозяйства. Грунтовые воды являются существенным источником водоснабжения. Весьма важен учет грунтовых вод.
Вода в грунте находится в различной форме:
1. Вода в форме водяного пара.
2. Гигроскопическая вода - впитана частицами грунта (выделяется при нагреве до 100˚С).
3. Пленочная вода - при увеличении влажности вода обволакивает зерна грунта пленкой и может передвигаться под влиянием молекулярных сил.
4. При дальнейшем увеличении влажности вода заполняет узкие поры и может передвигаться под действием сил капиллярного давления – это капиллярная вода.
5. В дальнейшем мы будем рассматривать только гравитационную воду, называя ее грунтовой водой.
Если под грунтовым потоком расположена пористая среда с рат, то такой поток безнапорный (со свободной поверхностью). Когда грунтовый поток вступает в пространство, ограниченное сверху и снизу водонепроницаемым пластом, то давление станет больше рат, движение будет напорным.
Фильтрация в начальном периоде происходит при неустановившемся движении, а через некоторый период времени - при установившемся.
Рассмотрим фильтрацию через мелкопористый грунт, когда просачивание медленное с очень малым числом Re, а поэтому движение воды будет ламинарным (ламинарная фильтрация).
Движение через гравий, гальку будет турбулентное (не рассматриваем).
Если фильтрация не зависит от направления движения, то грунт изотропный, в противном случае - анизотропный.
Напорная линия в случае грунтовой воды совпадает с пьезометрической, т.е. J=Jn
Понятия гидравлического и пьезометрического напоров совпадают:
H=Hn=z+P/γ
Рассмотрим трубу диаметра Д, заполненную песком и водой (рис. 1.102.). Под действием разности давлений на концах трубы вода движется (фильтруется) в этих порах.
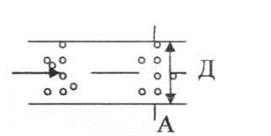
Рис. 1.102. Схема фильтрации.
Рассмотрим сечение А-А, на котором сосредоточены 3 площади:
1. Площадь сечения пор грунта ωпор - это площадь живого сечения потока.
2. Площадь сечения частиц грунта ωчаст.
3. Площадь сечения всей трубы ωгеом.
Тогда получаем:
. (172)
В отдельной поре эпюра скоростей имеет вид (рис. 1.103.), однако на практике с этим не считаются и «действительную скорость» находят по формуле:
Рис. 1.103. Схема фильтрации через грунт.
, (173)
где: Q - расход воды.
Наряду с этим вводят понятие - скорость фильтрации:
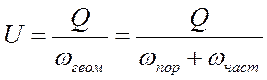. (174)
Под скоростью фильтрации понимают отношение объемного расхода жидкости Q, протекающей через сечение грунта, к общей площади этого сечения.
Как видно, скорость фильтрации U - есть фиктивная (воображаемая) скорость, получающаяся в том случае, если мы себе представим, что вода движется не только через поры; но и через частицы грунта, причем расход равен заданному (действительному расходу).
Проводя исследования. Дарси установил, что скорость фильтрации в случае установившегося движения может быть определена по формуле Дарси:
U=KJ, (175)
где, U- скорость фильтрации в точке потока;
J - пьезометрический уклон в той же точке;
К – коэффициент пропорциональности, называемый коэффициентом фильтрации.
Коэффициент фильтрации - это скорость фильтрации при уклоне J равном единице. Т.е. скорость фильтрации прямо пропорциональна уклону в первой степени.
Формула (174) относится к ламинарной фильтрации и имеет границы применимости.
Для воды, при вязкости ν = 0,01 см2/с, соотношение должно находиться в пределах:
Ud < 0,01…0,07, где, U – скорость, см/с,
d - средний диаметр частиц грунта, см.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.