Предмет гидравлика и основные физические свойства жидкости. Основные физические свойства жидкости. Понятие об идеальной жидкости, страница 24

где, C – коэффициент Шези, который определяется по формуле (60):

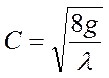,                                                                      где, λ – коэффициент  Дарси;

или по уже известной формуле (107):

.

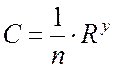Гидравлический расчет трубопроводов проводится с целью:

1.  Определение расхода жидкости Q при известных: d, l, H.

2.  Определение напора Н при известных: Q, d, l.

3.  Определение диаметра d при известных: Q, H, l.

В зависимости от величины потерь, по длине и местных, все трубопроводы можно разделить на: а) гидравлически длинные, б) гидравлически короткие.

Короткими трубопроводами называются трубопроводы, в которых местные потери напора являются основными и составляют не менее половины потерь напора по длине (h_{w м} >0,5  h_{w дл}).

Длинные трубопроводы – это трубопроводы, в которых основными являются потери по длине, местными и скоростными пренебрегают или берут в размере 5-10% от потерь по длине (как гидравлические короткие рассчитываются всасывающие линии насосов, сифоны).

В зависимости от условий работы и особенностей трубопроводов они разделяются на простые и сложные трубопроводы (рис. 1.82.).

Простой трубопровод состоит из труб одного или нескольких диаметров и не имеет разветвлений.

Сложный трубопровод состоит из магистрали с ответвлениями в разных точках.

Также различают тупиковые и кольцевые трубопроводы.

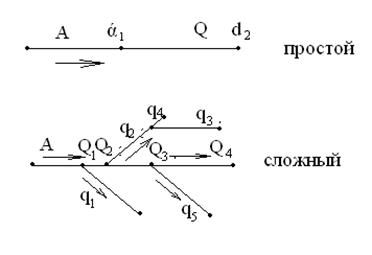
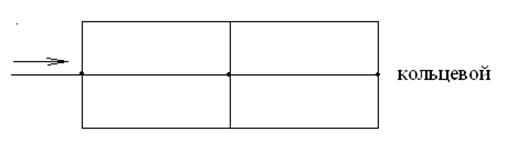
Рис. 1.82. Схемы трубопроводов.

Расчетные формулы.

При гидравлических расчетах трубопроводов широко используются понятия о расходных и скоростных характеристиках потоков.

Воспользуемся универсальной для обоих режимов движения жидкости формулой (92) - формулой Дарси для определения потерь напора:

;

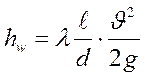и формулой Шези, (1.103.) для определения скорости:

.

Напишем выражение расхода в потоке, используя формулу Шези:

, или , где, K - расходная характеристика потока («модуль расхода»).

После подстановки K получаем формулы для определения расхода:

,                                                                              (142)

.                                                                         (143)

С другой стороны формулу Шези (скорости) можно записать:

или:

,                                                                               (144)

где, W - скоростная характеристика потока («модуль скорости»).

Так как уклон J – число безразмерное, то K имеет размерность расхода, а

W – размерность скорости.

K – представляет собой расход жидкости в русле заданного сечения при гидравлическом уклоне, равном единице.

Подставив в формулу  значение

, где, Н – напор, ℓ – длина, J – уклон.

и учитывая, что напор тратится на преодоление сопротивления, получим:

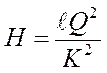                                                                                 (145)

Величина 1/К² при Q=1 численно равна напору, необходимому для преодоления сопротивления в трубопроводе при расходе Q=1.

Поэтому 1/К²=А  называют удельным сопротивлением  трубопровода.

По формулам, приведенным выше, для определения: Н и Q можно решить три ранее поставленные задачи, предварительно определяя коэффициент Шези С по формуле (142).

Для упрощения вычислений составлены таблицы для стандартных диаметров труб, где приведены коэффициенты: λ, С, К…

1.3.14.1.  Расчет гидравлически длинных трубопроводов

1. Расчет простого трубопровода, постоянного диаметра.

При напорном движении жидкости трубопровод работает полным сечением (), с постоянной средней скоростью  (равномерное движение), которая согласно формуле Шези равна: .

Рассматриваем трубопроводы, у которых местные потери напора малы, по сравнению с потерями напора по длине, поэтому ими можно пренебречь.

Для гидравлического расчета трубопроводов при турбулентном режиме движения используется уравнение Бернулли и формулы (92), (110), (111) «водопроводные формулы».

;    ;       .

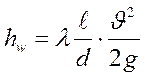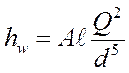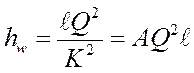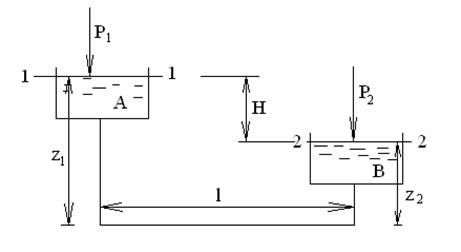
Рис. 1.83. Простой трубопровод постоянного диаметра.

Рассмотрим условия установившегося движения по трубопроводу, соединяющего два резервуара А и В.