Предмет гидравлика и основные физические свойства жидкости. Основные физические свойства жидкости. Понятие об идеальной жидкости, страница 30

Тип 1. Задачи, в которых задано сечение канала, т.е. в, h, m. Эти задачи решаются непосредственно без подбора искомой величины.

а)Дано: в, h, m, n, i.

Определить: Q = ?

Ход решения:

1.  Зная размеры, находим ω, χ;  ; .

2.  Находим R=ω/χ .

3.  Зная R, n , по таблице находим С; С= R^1/6/n.

4.  Зная С, R, определим υ , .

5.  Зная υ, ω , находим Q, .

б)       Дано: в, h, m, n, Q.

Определить: i = ?

Ход решения:

1.  Как и выше находим ω, χ, R, C.

2.  Зная ω, находим υ; .

3.  Зная υ, C, R , определим i; .

Тип 2. Задачи, в которых живое сечение не задано, т.е. искомые в, h (рис. 1. 98., 1. 99.).

Задачи этой группы решаются путем подбора искомой величины.

а)       Дано: в, m, n, I, Q.

Определить h = ?

Рис. 1. 98. К определению глубины канала.

Ход решения:

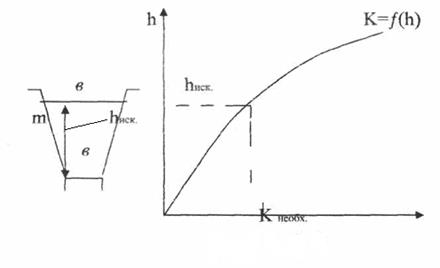
1.  Находим модуль расхода (необходимый) К_необх ,_.

2.  Составляем таблицу, задаваясь переменой h и вычисляя модуль расхода К; (h, mh, χ, R, C, K); .

3. По данным    h и К строим график K=ƒ(h).

4.  Зная К_необх, находим h_иск по графику.

б)                Дано: m, h, n, I, Q.

Определить    в = ?   (по дну)

1.  Находим необходимый модуль расхода К_необх , .

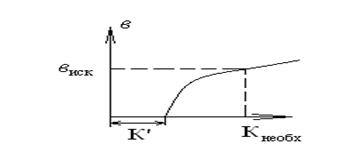
2.  Составляем таблицу, задаваясь переменной в   и определяя К,

(в, ω, χ, R, C, K); .

Рис. 1. 99. К определению ширины канала.

3. По данным строим график и находим искомое.

К'- соответствует треугольному руслу.

1.3.17. Водосливы

Общие понятия.

Если поток жидкости со свободной поверхностью преградить какой-либо стенкой, то жидкость, уровень которой перед преградой повысится, начнет переливаться через стенку (порог, ребро, уровень) по всей ее ширине или, при наличии выреза в стенке, через порог такого выреза.

Водослив - сооружение в той части, где жидкость переливается через гребень.

Движение жидкости - истечение через водослив.

Область потока, находящаяся перед сооружением, называется верхним бьефом, а за ним нижним бьефом.

Терминология и классификация водосливов.

Наметим на расстоянии ℓ_в от верховой грани водосливной стенки сечение в-в, в котором начинается спад поверхности (рис. 1.100.).

Как показывают опыты, длина , где величина Н, измеряемая сечением «в-в», - геометрический напор на водосливе.

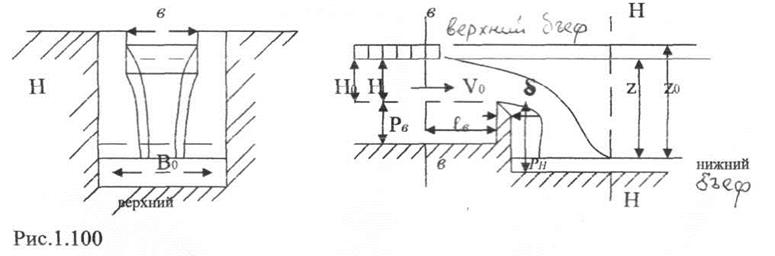Геометрический напор Н на водосливе - представляет собой превышение над гребнем водослива уровня воды в сечении «в-в» , где еще нет спада свободной поверхности, обусловленного истечением воды через водослив.

Примем следующие обозначения:

в -ширина водослива, или иначе, ширина водосливного отверстия;

δ -толщина водосливной стенки;

Рв -высота водослива со стороны верхнего бьефа;

Рн -высота водослива со стороны нижнего бьефа, в случае Рв = Рн эту высоту обозначив через Р;

В₀   -ширина русла, где устроен водослив;

z -геометрический перепад на водосливе, разность уровней воды в верхнем и нижних бьефах;

υ₀ - скорость подхода, т.е. скорость в сечении в-в;

Н₀ -полный напор на водосливе, или напор с учетом скорости подхода;

 - полный перепад на водосливе, или перепад на водосливе с учетом скорости подхода;

;

α - коэффициент неравномерности распределения скоростей равный 1,0…1,1;

g -ускорение силы тяжести,   g= 9,81 м/с.

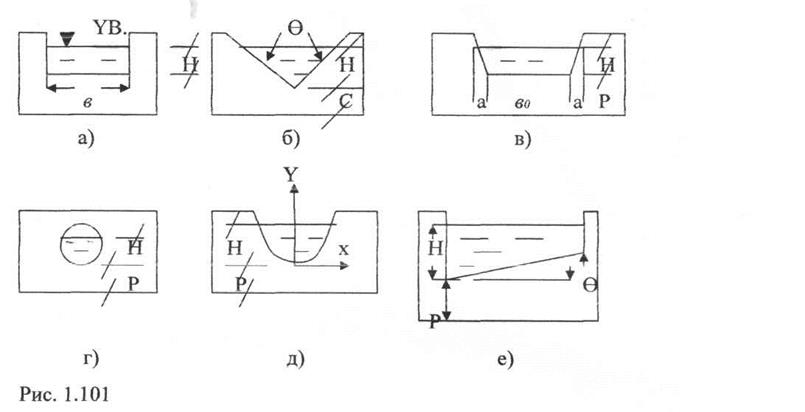
В зависимости  от  геометрической  формы  водосливного отверстия, различают следующие виды водосливов (рис 1.101.): а) прямоугольные; б) треугольные; в) трапецеидальные; г) круговые; д) параболические; е) с наклонным гребнем.

 

1.3.17.  Фильтрация. Основной закон фильтрации

Водопроницаемый грунт состоит из отдельных частиц (песчинок), между которыми имеются поры. Суммарный объем пор составляет часто 35-40 % от объема всего грунта.

Фильтрация - явление движения воды в порах грунта.

Объем грунтовых вод составляет порядка 10 млн. км³., т.е. 1% от объема воды мирового океана.