Предмет гидравлика и основные физические свойства жидкости. Основные физические свойства жидкости. Понятие об идеальной жидкости, страница 18

Если  - гидравлически шероховатые трубы.

Коэффициент гидравлического сопротивления трения. Области трения.

Коэффициент гидравлического сопротивления трения  - коэффициент Дарси, является функцией зависящей от числа Рейнольдса, а в некоторых случаях и от относительной шероховатости:

.

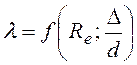Исследованиями установлено, что при различных режимах движения жидкости (рис. 1.66., 1.67., 1.68.)      определяется по различным формулам, при этом турбулентный режим делится на несколько областей.

1.  Так при ламинарном движении,  и , можно воспользоваться выражением (91):

.

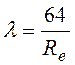2.  В области гидравлически гладких труб, , возможны два варианта:

а) если, , то можно воспользоваться эмпирической формулой Блазиуса:

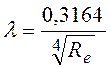.                                                                               (96)

б)  если,  ; 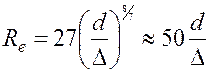, то можно воспользоваться формулой Филоненко:

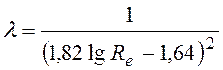.                                                            (97)

Т.е. коэффициент Дарси, для гладких труб, при турбулентном режиме движения жидкости, не зависит от шероховатости, а зависит только от .

В практике гидравлически гладкие трубы встречаются крайне редко.

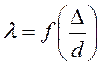3.  В области гидравлически шероховатых труб или квадратичной область сопротивления, при  и , можно воспользоваться формулой Прандиля - Никурадзе:

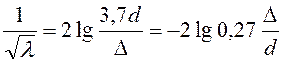 ;                                                 (98)

или формулой Шифферсона:

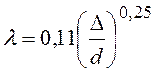.                                                                        (99)

4.  Но существует еще и переходная область, расположенная между областью гидравлически гладких труб и областью гидравлически шероховатых труб, 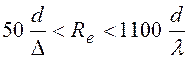, , 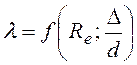в данной области можно воспользоваться формулой Альтшуля:

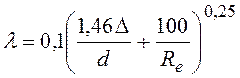,                                                          (100)

или:

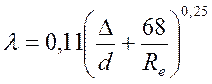.                                                              (101)

Коэффициент  и  уменьшается с увеличением числа , но не одинаково, так как по разному влияет вязкость на сопротивление трению (при турбулентном меньше).

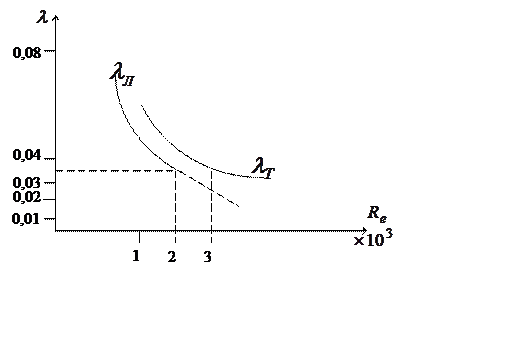
Рис. 1.66.  К определению коэффициента трения.

 

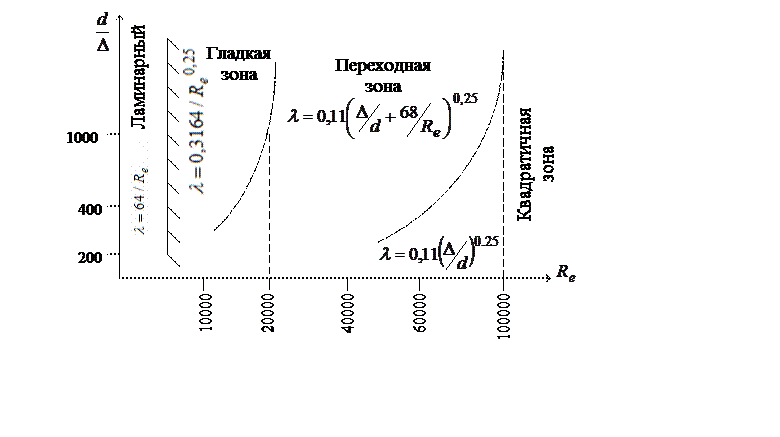Рис. 1.67.  Области сопротивления.

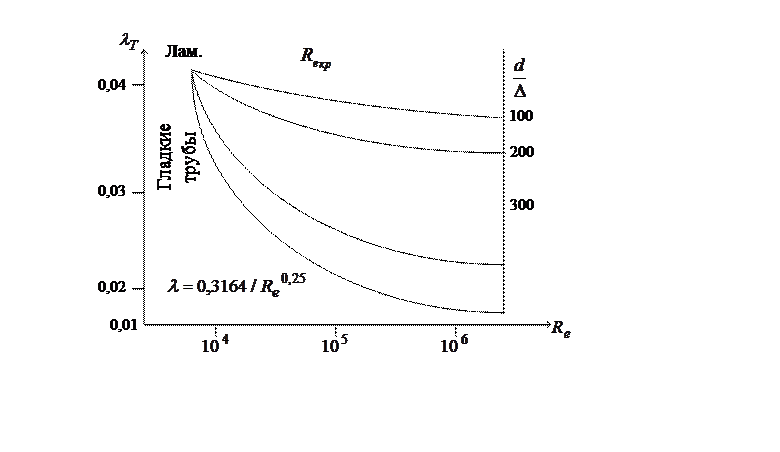
Рис. 1.68  График зависимости коэффициента трения от режима движения и шероховатости.

Из основного уравнения равномерного движения (67) имеем:

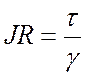,  но .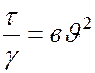   

Или получаем:                   

,                                                                              (102)

где:    - коэффициент пропорциональности;

 - гидравлический уклон;

R- гидравлический радиус;

 - удельная сила трения.

Тогда среднюю скорость движения жидкости можно определить по формуле:

.

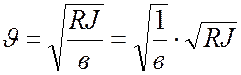Если принять, что:

, м²/с,

где: С - коэффициент Шези.

Получаем формулу Шези:

 .                                                                           (103)                    

Тогда выражение (41),для определения расхода приобретает вид:                              .                                                                         (104)

Введя показатель К - расходная характеристика, получаем:

,                                                                              (105)

где:    , м³/с.                                                                  (106)

На практике пользуются следующими расчетными (эмпирическими) формулами:

Формула Павловского ():

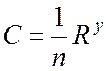,                                                                                (107)

где,  - коэффициент шероховатости;

 - гидравлический радиус;

 - показатель степени (зависит от  и ). .

Для приближенных расчетов можно брать:

при ; , при ; .

Формула Маниинга:

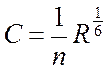 .                                                                               (108)

Эта формула дает наиболее точные результаты, при расчете трубы  - берется из справочника (коэффициент шероховатости из таблицы Павловского)  - 0,012.

 - абсолютная шероховатость, эквивалент  (0,010,03).

1.  для цельнотянутых латунных и медных труб:

;

2.  для новых стальных труб:

;

3.  для стальных труб бывших в эксплуатации:

;