Неравномерное движение можно разделить на два вида:
а) плавно изменяющееся движение - живое сечение можно считать плоским; б) резко изменяющееся движен, - живое сечение не плоское.
Установившееся неравномерное параллельно-струйное движение потока, при котором угол расхождения между линиями тока и их кривизны – величины малые, называется медленно-изменяющимся (плавно-изменяющимся) движением. (Рис. 1.40).
Распределения давлений в плоскостях поперечных сечений потока, удовлетворяющих условиям плавно меняющегося движения, происходит по основному закону гидростатики.
Рис 1.40. Плавно изменяющееся движение.
По воздействию давления на поток жидкости, движение делится на: напорное, безнапорное и свободные струи.
Напорное - движение жидкости под действием гидродинамического давления и силы тяжести (рис. 1.41.).
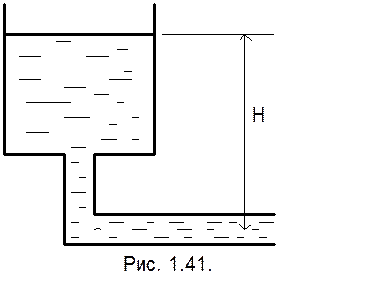
Напорное движение.
При напорном движении поток не имеет свободной поверхности.
Безнапорное движение происходит только под действием силы тяжести (рис. 1.42.).
Безнапорное движение – это движение со свободной поверхностью.
Свободная струя жидкости - поток (струя), не ограниченный твердыми стенками (струи брандспойта).
1.3.4. Уравнение неразрывности для установившегося
движения жидкости
Дифференциальное уравнение неразрывности характеризует известное положение, что при движении жидкости в ней не образуется ни разрывов сплошности, ни пустот.
Уравнение неразрывности для элементарной струйки и потока являются математическим выражением условий сплошности течения при установившемся движении (Рис. 1.43).
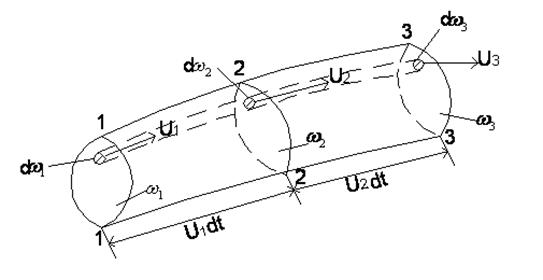
Рис. 1.43. К уравнению неразрывности.
Уравнение неразрывности для элементарных струек:
u1dω1 = u2dω2 = u3dω3 = const. (50)
Или: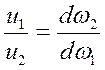 
.
Уравнение неразрывности показывает, через все сечения элементарной струйки в единицу времени проходит одно и то же количество жидкости, а скорости обратно пропорциональны площадям соответствующих живых сечений.
Уравнение неразрывности потока (постоянства расхода):
υ1ω1 = υ2ω2 = υnωn,
Q = ω1υ1 = ω2υ2 = const. (51)
Уравнение неразрывности потока показывает, что в разных сечениях могут меняться скорость (υ) и площадь (ω) сечения, а расход (Q) вдоль потока остается постоянным
.
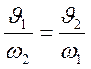1.3.5. Уравнение Бернулли
В 1738 г. действительный член Петербургской академии Даниил Бернулли, применив к движущейся жидкости «закон кинетической энергии», получил свое знаменитое уравнение, связывающее скорость и гидродинамическое давление в движущемся потоке.
Рассмотрим отсек идеальной жидкости АВ, заключенной в элементарной струйке между сечениями 1-1 и 2-2 (рис. 1.44.).
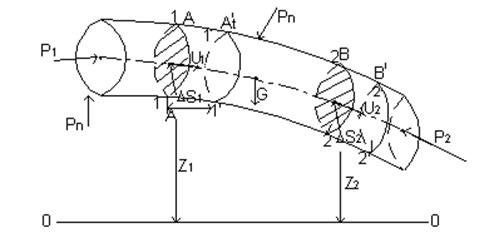
Рис. 1.44. К уравнению Бернулли.
Где: dω1, dω2 – площади живых сечений струйки 1-1, 2-2;
U1, U2 – скорости движения частиц в сечениях.
Обозначим Z1, Z2 геометрические высоты центров тяжести площадей живых сечений струйки над плоскостью сравнения 0-0.
p1, p2 – гидродинамическое давление в сечениях. Для бесконечно малых dω1 и dω2 скорости U1 и U2 и гидродинамическое давление p1, p2 можно принимать одинаковыми для всех частиц в рассматриваемых сечениях.
После преобразований получаем уравнение Бернулли для элементарной струйки идеальной жидкости - устанавливающее связь между скоростью движения, гидродинамическим давлением и геометрической высотой точек (рис. 1.45.):
.
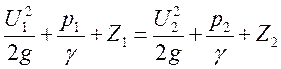(52)
Геометрический смысл уравнения Бернулли.
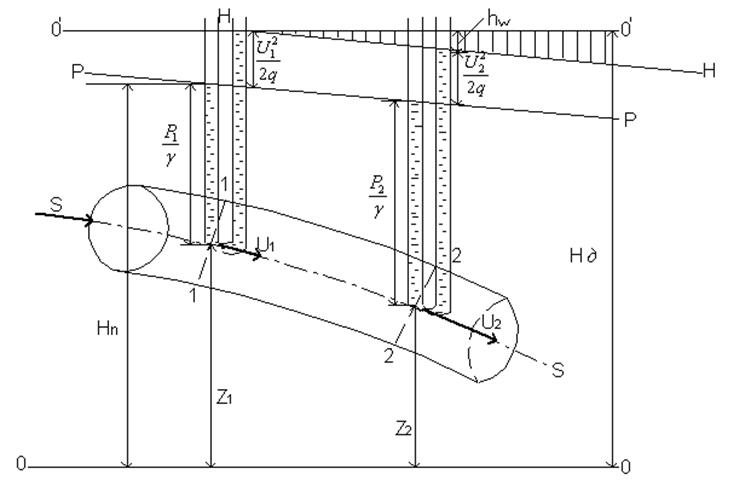
Рис. 1.45. Смысл уравнения Бернулли.
Напорная плоскость - горизонтальная плоскость, проведенная через точки О′-О′.
Напорная линия - линия, соединяющая точки О′-О′ (уровень жидкости в трубках Пито в различных сечениях).
Если Н-Н совпадает с О'-О' – идеальная жидкость.
Пьезометрическая линия – линия (р-р), соединяющая уровни жидкости в пьезометрах.
Гидродинамический напор Н
над плоскостью сравнения для элементарной
струйки идеальной жидкости определяется по формуле:
Н = 
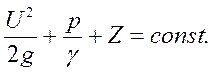(53)
Следовательно, напорная плоскость проходит на высоте гидродинамического напора. В этом и есть геометрический смысл уравнения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.