Предмет гидравлика и основные физические свойства жидкости. Основные физические свойства жидкости. Понятие об идеальной жидкости, страница 7

В данном случае плоскость АС воздействует сила Р₁, которую можно определить из уравнения (29), она равна:

Р₁ = ½ h ∙ h ∙ b ∙ γ = 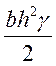и приложена на 1/3 h от дна.

Вертикальная сила Р₂ реакции дна, равна силе давления на дно, но противоположно направлена:

Р₂ = ℓ ∙ b ∙ h ∙ γ, где:  ℓ – длина СВ,

b  - длина стенки.

Сила Р₂  - приложена в центре площадки СВ.

Сила тяжести жидкости в рассматриваемом объеме АСВ приложена в его центре тяжести и равна:

G = b ω γ,    где:  ω  - площадь фигуры АВС.

Все эти силы находятся в равновесии и поэтому должны образовать замкнутый многоугольник (рис. 1.25). Из многоугольника определим величину и направление силы  Р:

Р = .                                                                (32)    

tg β = 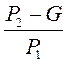.                                                               (33)

Р = .                                                                         (34)

Разрывающие силы в трубе круглого сечения (без учета собственного веса), отрывающие полуцилиндры, равны произведению манометрического давления на площадь диаметральных сечений (рис. 1.26.).

Р = рω = рDℓ = 2р ∙ r ℓ.                                                                     (35)

Тогда для расчета стенки получаем: 

2рrℓ = 2 ℓσs  , где:    σ – разрывающее напряжение, ,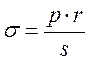

s – толщина стенки.

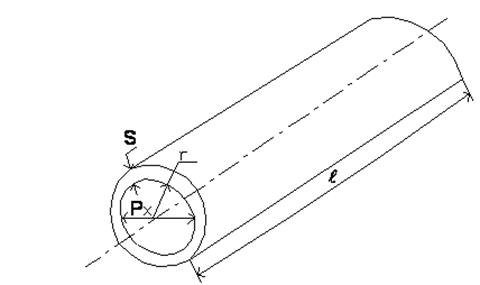
Рис. 1.26. К определению толщины стенки.             

Эпюры давления на криволинейные поверхности.

Если брать γ = 1 тс/м³, то ордината давления в любой точке = h (глубине погружения).

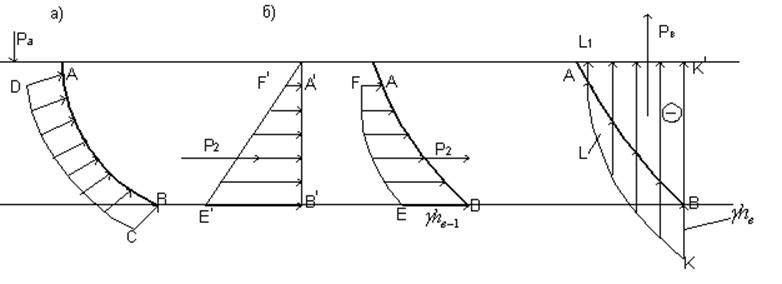
Рис. 1.27  Эпюры давления на криволинейные стенки.

а) распределение давления АВСД имеет разную направленность –поэтому невозможно использовать для определения Р (силы давления).

б) строим отдельно эпюры горизонтального и вертикального давления (постоянное в т. в любых направлениях). АВЕF – эпюры горизонтального манометрического давления. А' В', Е', F' – выпрямлены эпюры горизонтального давления на вертикальную проекцию поверхности АВ.

1.  Эпюра горизонтального давления зависит только от величины вертикальной проекции и глубины погружения и не зависит от формы поверхности.

2.  Горизонтальная составляющих Р равна произведению давления р на площадь вертикальной проекции: Р = γh ∙ ω_х

в) АВКL – эпюры вертикального манометрического давления на АВ. АВК'L' – равновеликая (закон Архимеда).

1.  Р_z (вертикальная составляющая) равна весу жидкости в объеме АВК₁L₁ (тело давления):

Р_z = γ ∙ W_{АВК‚L‚}

2.  Точка приложения в центре тяжести объема.

Пользуясь правилом сложения векторов:

Р =

1.2.9. Закон Архимеда. Плавание и остойчивость тел

Закон Архимеда - на тело, погруженное в жидкость, действует выталкивающая сила (подъемная), направленная вверх и равная весу жидкости, вытесненной этим телом.

Архимедова сила определяется по формуле:

Р = γV,                                                                                       (36)   

где:    γ – удельный вес жидкости,

V – объем вытесненной жидкости.

Cила Р, проходит через центр тяжести вытесненного объема жидкости -центр водоизмещения.

Водоизмещение – вес вытесненной жидкости.

Задача о плавании тел сводится к изучению:

1.  Плавучести тел – свойства тела плавать при данной нагрузке, имея заранее установленное погружение (закон плавучести).

2.  Остойчивости тел – способности возвращаться в исходное положение после прекращения действия силы, вызывающей крен.

Обозначим  G – вес тела,  P - Архимедова сила то если:

G < P  - тело всплывает,

G > P  - тело тонет,

G = P  - тело плавает во взвешенном состоянии.

Если тело плавает на поверхности, то плавание называется надводным, в противном случае подводное.

Объемное водоизмещение - объем жидкости, вытесняемый плавающим телом.

Ось плавания - линия, проходящая через центр тяжести и центр водоизмещения, соответствующий нормальному положению.

Плоскость плавания - плоскость свободной поверхности жидкости, пересекающая плавающее тело.

Остойчивость.Условие остойчивости зависит от положения точек Д – центр водоизмещения и С – центр тяжести (подводное).