Предмет гидравлика и основные физические свойства жидкости. Основные физические свойства жидкости. Понятие об идеальной жидкости, страница 13

Пьезометрический уклон_р - падение пьезометрической линии на единицу длины потока (p-p).

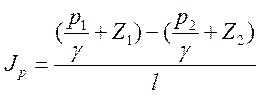.                                                      (62)

При равномерном движении  J = J_p.

1.3.7. Основное уравнение равномерного движения

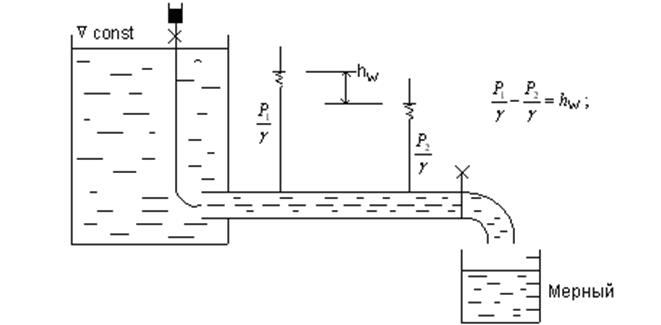
Движение жидкости в водопроводах, нефтепроводах, бензо- и маслопроводах, а также в открытых каналах во многих случаях является равномерным, т.е. таким, при котором скорость и глубина по длине потока постоянны (рис. 1.49.).

Для вывода основного уравнения рассмотрим поток жидкости с постоянным сечением ω и наклоненный к горизонту под углом  α_о.

Выделим в потоке сечением 1-1 и 2-2 отсек  АВСД  длиной  , обозначим:

Гидродинамическое давление через  p₁ и p₂.

Геометрические высоты через  Z₁ и Z₂ , тогда sin α_o = .

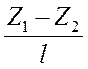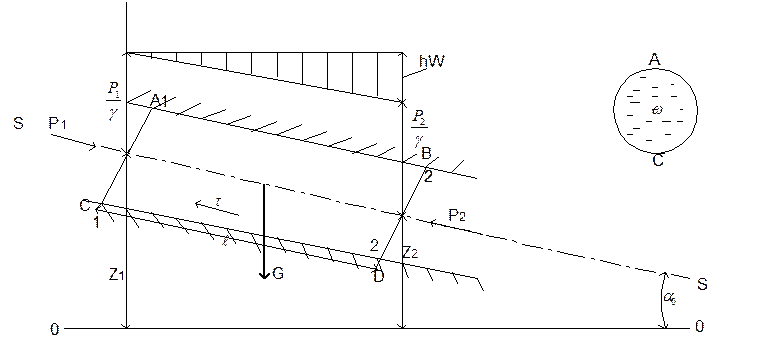
Рис. 1.49.  К уравнению равномерного движения.

Внешние силы, приводящие жидкость в движение, в условиях равномерного движения, должны быть равны силам сопротивления, возникающим при движении, или суммы проекций внешних сил на любую ось должны равняться сумме проекций сил сопротивления.

Если за ось проекций принять ось потока, то в уравнение войдут следующие силы:

а) гидродинамического давления - p₁ = ωp₁;    p₂ = ωp₂;

б) силы тяжести отсека  - G = γω

в) силы сопротивления (силы трения) - Т_тр = τ_о, где:    τ_о – удельная сила трения (на единицу поверхности),

χ  - смоченный периметр.

Составим уравнение равновесия  сил:

Р₁ – Р₂ + G sinα_o – Т_тр = 0.

После подстановки получаем:

p₁ω – p₂ω +

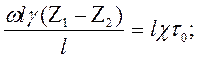
Разделив обе части уравнения на γω, получаем основное уравнение равномерного движения жидкости:

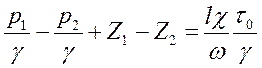.                                                      (63)

Или:

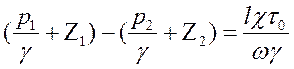.                                                (64)

Так как кинетическая энергия 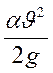 в обоих сечениях одинакова (равномерное движение), то левая часть уравнения является разностью удельных энергий и выражает потери энергии на длине отсека, т.е.:

Э₁ – Э₂ = h_w = .                                                             (65)

Данное уравнение является основным уравнением равномерного движения и служит для определения потерь энергии по длине потока.

Таким образом, сопротивления, возникающие при равномерном движении вязкой жидкости, прямо пропорционально длине потока, смоченному периметру, удельной силе трения на стенке и обратно пропорционально площади живого сечения потока.

Но отношение площади сечения  к смоченному периметру, есть гидравлический радиус  R = .

Введя гидравлический радиус в уравнение (65), получим:

h_w = .                                                                                  (66)

Разделим обе части уравнения на  и исходя из того что, отношение 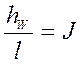 - это гидравлический уклон, получаем:

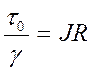.                                                                                  (67)

Основное уравнение равномерного движения показывает, что  касательное напряжение, отнесенное к объемному весу жидкости, равно произведению гидравлического радиуса  R  на гидравлический уклон  J, где касательное напряжение – это внутреннее трение.

Из основного уравнения равномерного движения следует, что касательное напряжение прямо пропорционально потерям напора.

Опыты показывают, что касательное напряжение а, следовательно, и потери напора зависят от скорости течения жидкости, а также от режима движения.

1.3.8. Два режима движения жидкости. Гидродинамическое

подобие.Кавитационные течения

Рядом исследователей, в частности Хагеном в 1839 и 1854 г.г. и Менделеевым в 1880 г., было замечено два принципиально разных режима движения жидкости. Наиболее полное исследование в данной области провел английский физик Рейнольдс в 1883 г. (рис. 1.50.).

Было установлено, что в природе существует два режима движения жидкости: ламинарный (слой) и турбулентный (беспорядочность).

При ламинарном режиме движения поток жидкости движется отдельными струйками или слоями и траектории их не пересекаются.

При турбулентном режиме движения струйчатость потока нарушается, траектории движения сложные и пересекающиеся.