dP = pdω; или dP = pdω = (Po + γh)dω;
где Р – гидростатическое давление.
 |
Т.е. получаем, что сила суммарного давления на плоскую наклонную стенку равна сумме параллельных непрерывно изменяющихся сил, т.е. интегралу в пределах всей смоченной поверхности (площади).
Р = роω + γ∫hda ,
ω
где: h = у sin α.
Тогда интеграл можно представить:
∫ hdω = sin α ∫ уdω,
ω ω
где: ∫ уdω – есть статический момент площади относительно оси ОХ равный произведению площади ω на уцт.
Тогда: ∫ уdω = уцт ∙ ω;
∫ hdω = sin α ∫ уdω = sin α уцт ∙ ω = hцт ∙ ω.
Окончательно получаем:
Р = р0ω + γ hцт ∙ ω = ω (р0 + γ hцт). (26)
Если р0 = ра, то:
Р = γ hцт ∙ ω. (27)
Т.е. сила давления на плоскую стенку равна по величине произведению площади смоченной стенки на давление испытываемое ее центром тяжести.
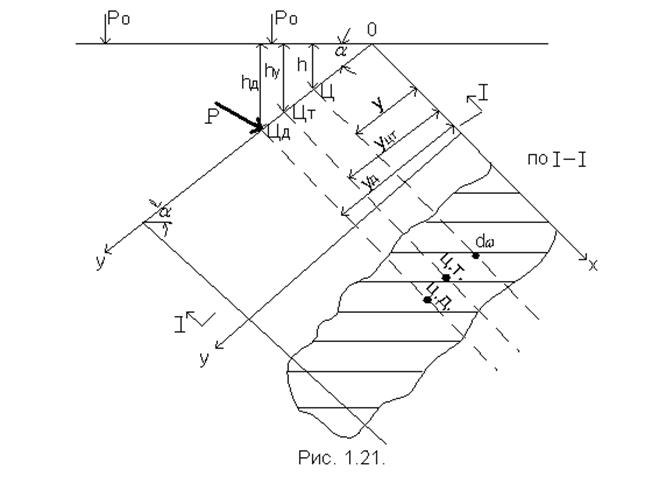
Определение центра давления.
Кроме величины и направления силы необходимо определить и точку приложения равнодействующей. Считая р0 = ра, определим на каком расстоянии уд от свободной поверхности жидкости, вдоль смоченной плоскости, находится точка приложения центра давления Цд.
Будем исходить из положения, что момент равнодействующей силы, относительной любой оси, равен сумме моментов сил, составляющих относительно той же оси. За ось моментов возьмем линию уреза жидкости, т.е. ось ОХ.
М = Р ∙ уд = ∫ у ∙ dP;
Учитывая, что
Р = ωγhцт, а dP = γhdω = γу sin α ∙ dω;
Имеем:
М = γhцт ∙ ω ∙ уд = γ sin α ∫ у2dω = γ sin ∙ Jx;
Где: Jx = ∫ у2 ∙ dω – момент инерции смоченной площади относительно ОХ.
Из этого следует: уд = 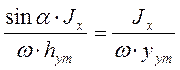 .
.
Эту формулу можно преобразовать, так как
Jx = Jo + ωуцт2, где: Jx – момент инерции относительно произвольной оси Х,
Jo – момент инерции площадки, относительно оси, проходящей через центр тяжести.
Или окончательно:
уд = 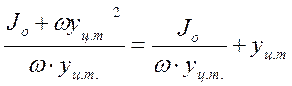 . (28)
. (28)
Следовательно, центр избыточного давления всегда
распложен ниже центра тяжести на величину (по наклону) равную отношения 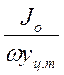 .
.
Если щит расположен горизонтально, то центр давления совпадает с центром тяжести щита.
1.2.7. Эпюры гидростатического давления
на плоские поверхности
Эпюра - диаграмма распределения давления (графический способ определения силы давления).
Рассмотрим плоскую вертикальную стенку (рис. 1.22.).
Для определения суммарного избыточного гидростатического давления воспользуемся формулой (27):
Р = ωγhц.т = bhγ![]()
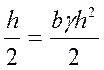 . (29)
. (29)
Сила Р = 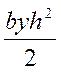 - представляет площадь эпюры
гидростатического давления
- представляет площадь эпюры
гидростатического давления ![]() , умноженную на
ширину пластины b (рис. 1.22.).
, умноженную на
ширину пластины b (рис. 1.22.).
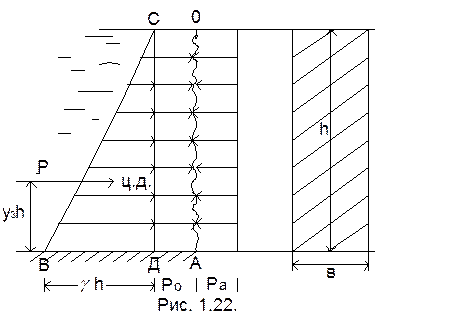
Площадь треугольника ВСД – это избыточное давление.
Площадь фигуры ВСОАД – полное гидростатическое давление.
Центр тяжести эпюры – это центр приложения силы.
Если щит наклонный (рис. 1.23.), то эпюра избыточного давления р = γh изобразится в виде треугольника ОАВ и суммарная равнодействующая сила будет равна:
Р = 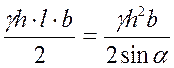 , (30)
, (30)
Т.к. 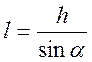 .
.
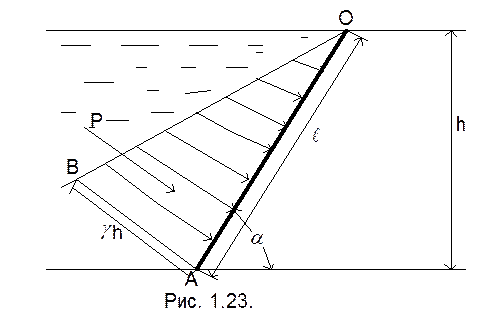
Если давление с двух сторон (рис. 1.24.), то:
Р = γb (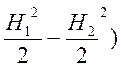 (31)
(31)
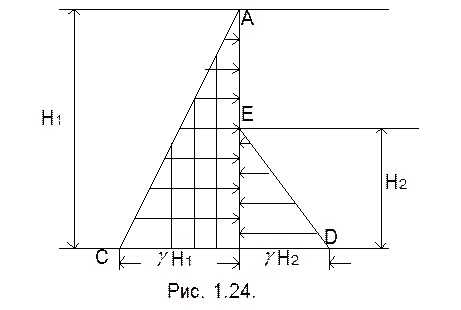
1.2.8. Давление жидкости на криволинейные поверхности
Давление жидкости на плоскую стенку складывается из элементарных давлений на элементарные площади. При этом силы давления параллельны и их можно было свести к одной равнодействующей.
Для криволинейной поверхности, только в частных случаях можно найти равнодействующую. Из криволинейных поверхностей в практике чаще встречаются цилиндрические, которые и рассмотрим. Определим силу давления на цилиндрическую поверхность АВ с образующими длиной b. Из жидкости выделим ограниченный объем САВ плоскостями АС и СВ. Отбросим остальную жидкость и заменим ее соответствующими силами (рис. 1.25).
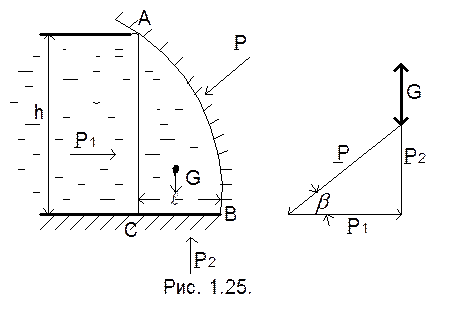
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.