Предмет гидравлика и основные физические свойства жидкости. Основные физические свойства жидкости. Понятие об идеальной жидкости, страница 10

Живое сечение - поверхность в пределах потока, проведенная нормально к направлению струек (рис. 1.34.).

Площадь живого сечения струйки - площадь поперечного сечения струйки жидкости, перпендикулярного к внутренним линиям тока (dω).  

Площадь живого сечения потока - площадь поперечного сечения потока жидкости, перпендикулярного элементарным струйкам (ω).  

При параллельно-струйном движении живое сечение является плоским, при плавно изменяющемся движении, живое сечение имеет кривизну.

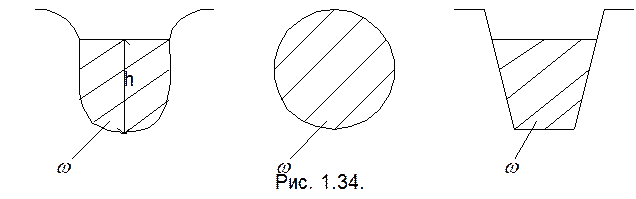
Средняя скорость в живом сечении – это такая скорость (υ), с которой должны двигаться все частицы жидкости в потоке, так, чтобы количество жидкости, протекающей через рассматриваемое живое сечение, было равно действительному количеству жидкости, протекающей через это сечение, при действительных скоростях течения (U).

Расход жидкости - количество жидкости, протекающее через площадь поперечного сечения за единицу времени.

Различают: объемный - Q, весовой - G и массовый - М расходы.

dQ =  U dω, м³/с.                                                                      (37)

dG = γdQ, Н/с.                                                                          (38)

dM = ρdQ, кг/с.                                                                         (39)

Элементарный расход струйки будем обозначать иди dQ или q.

Для потока конечных размеров в общем случае скорость имеет различное значение в различных точках сечения, поэтому:

Q = ∫ Udω.                                                                                (40)

Пока нет аналитических зависимостей для всех случаев (условий) движения U = f (у,z) (рис. 1.35.):

Q = υω,                                                                                     (41)  

где: υ – средняя скорость. 

υ = 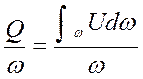.                                                                   (42)

Так как для большинства случаев интеграл не решается.

Рис. 1.35. Эпюра скорости.

Смоченный периметр – периметр поперечного сечения потока в пределах соприкосновения с ограждающими его стенами, исключая поверхность, отделяющую жидкость от газообразной среды (χ).

Для прямоугольного сечения (рис. 1.36.) смоченный периметр определяется по формуле:

χ = b + 2h.                                                                                (43)

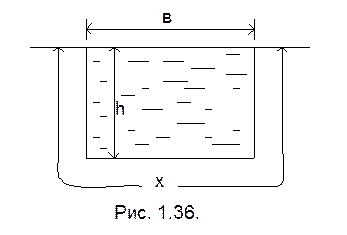
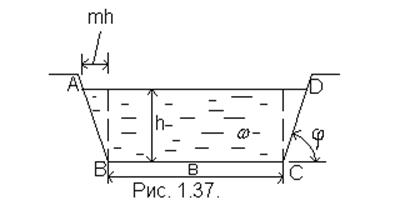
Для трапецеидального сечения (рис. 1.37.):

χ = b + 2h.                                                                   (44)

Исходя из того, что:

АВ =, где:    m = ctg φ – коэффициент заложения откоса.

Для круглого сечения:

χ = 2πr = πD.                                                                           (45)

Гидравлический радиус - отношение площади живого сечения (ω) к смоченному периметру (χ).

R = .                                                                                      (46)   

Для прямоугольного сечения: 

R =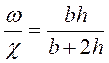.                                                                         (47)

Для круглого сечения:

R = 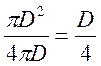 .                                                                         (48)

Для трапецеидального сечения:

R = 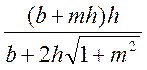.                                                                  (49)

С учетом того, что:

 ω = [b + (b + 2mh)] ∙  = (b + mh) h.

1.3.3. Виды движения жидкости

Существует два вида движения:

1.  Установившееся движение жидкости:

,

.

2.  Неустановившееся движение жидкости (истечение из бочки при переменном уровне жидкости  Н):

U = f₁ (x, у, z, t),

Р = f₂ (x, у, z, t)

Установившееся движение может быть равномерным и нерановмерным.

Равномерное движение - установившееся движение, при котором поперечное сечение потока (ω) и средняя скорость (υ) и давление (р) одинаковы по всей длине потока.

При неравномерном движении живое сечение, средняя скорость и давление изменяются по длине потока (рис. 1.38.).

                               

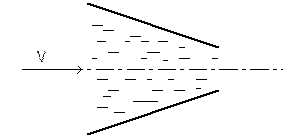
Неравномерное                                              

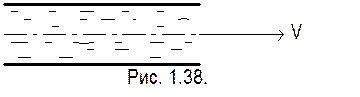Равномерное

Равномерное движение является параллельно-струйным движением, живое сечение ω плоское, υ_ср = const  (рис. 1.39.).

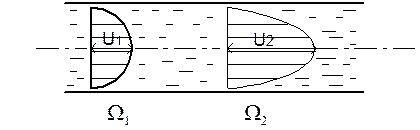
Рис. 1.39.  Эпюра скорости.