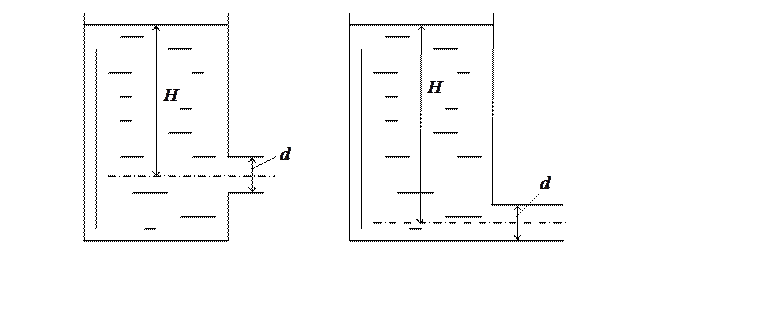
Рис. 1.70. Схема отверстий.
3. Полное сжатие – когда струя получает сжатие по всему периметру, и не полное, когда струя с некоторых сторон не испытывает сжатия.
Полное сжатие разделяют на:
а) совершенное;
б) несовершенное.
Если границы сжатия отверстия удалены достаточно и стенки не влияют на истечение – совершенное сжатие.
Если же отверстие близко от стенки или поверхности – это отверстие с несовершенным сжатием.
Для круглого отверстия ![]() (рис.
1.71.), а для прямоугольного сечения
(рис.
1.71.), а для прямоугольного сечения ![]() и
и ![]() .
.
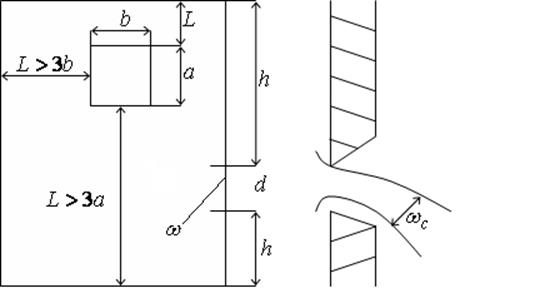
Рис. 1.71 Схема истечения через отверстие.
Коэффициент сжатия струи ![]() определим
по формуле:
определим
по формуле:
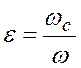 , (118)
, (118)
где, ![]() - площадь сечения
отверстия;
- площадь сечения
отверстия;
![]() - площадь сжатого
сечения.
- площадь сжатого
сечения.
Для небольших размеров отверстия ![]() .
.
Коэффициент сжатия ![]() - имеет
большее значение для несовершенного и неполного сжатия, меньшее для
совершенного и полного сжатия.
- имеет
большее значение для несовершенного и неполного сжатия, меньшее для
совершенного и полного сжатия.
Инверсия струи.
При истечении струи из круглого отверстия, квадратного
или треугольного - струя не сохраняет его форму, и вследствие действия сил
поверхностного натяжения постепенно деформируется. Это изменение формы и есть инверсия
струи. Исходя из этого ![]() - для различных форм отверстий
можно принимать одинаковым.
- для различных форм отверстий
можно принимать одинаковым.
Истечение жидкости через малые отверстия в тонкой стенке.
Гидравлически тонкая стенка – это острые края, не влияющие на форму струи. При истечении жидкости через отверстие, траектории частиц в отверстии непараллельные.
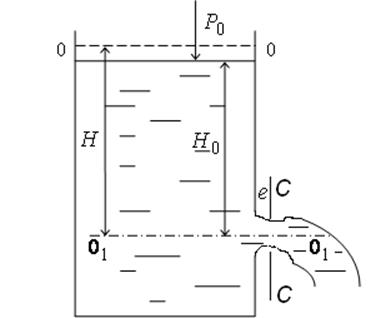
Рис. 1.72. Схема истечения.
Благодаря криволинейному движению, давление по сечению увеличивается от краев к центру, а скорости наоборот уменьшаются.
Составим уравнение Бернулли для потока (рис. 1.72.), сравнивая
сечения ![]() ,
, ![]() ,
, ![]() , при этом
, при этом ![]() -
проходит через центр тяжести сечения;
-
проходит через центр тяжести сечения;
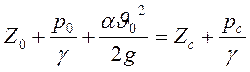 +
+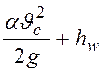 ;
;
где, ![]() - скорость в сечении
отверстия;
- скорость в сечении
отверстия;
![]() -
скорость в сжатом сечении;
-
скорость в сжатом сечении;
![]() ,
, ![]() - давление в сечении;
- давление в сечении;
![]() -
потери напора (местные в данном случае).
-
потери напора (местные в данном случае).
Если ![]() , то
, то 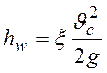 (местные потери).
(местные потери).
Обозначим через ![]() полный
напор
полный
напор
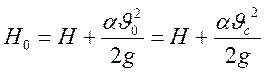 ;
;
Тогда,
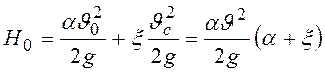 .
.
Из полученного выражения определим среднюю скорость в сжатом сечении (формула Торичелли):
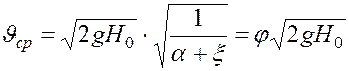 , (119) где,
, (119) где, 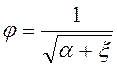 - коэффициент
скорости для круглого отверстия в тонких стенках,
- коэффициент
скорости для круглого отверстия в тонких стенках, ![]() = 0,97
= 0,97![]() 0,98.
0,98.
Определим расход ![]() ,
,
![]() . (120)
. (120)
Введя понятие коэффициент расхода -![]() получаем:
получаем:
![]() . (121)
. (121)
Для малых отверстий ![]() .
.
Затопленное отверстие (истечение под уровень).
При истечении из отверстия в тонкой стенке под уровень образуется сжатое сечение С-С, в котором гидродинамическое давление подчиняется гидростатическому закону, следовательно, можно написать уравнение Бернулли для сечений (рис. 1.73.).
Для плоскости сравнения 0-0 получаем:
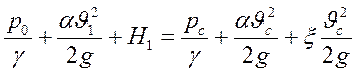 ;
;
Пренебрегая членом 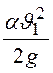 и
определяя
и
определяя ![]() , можно записать:
, можно записать:
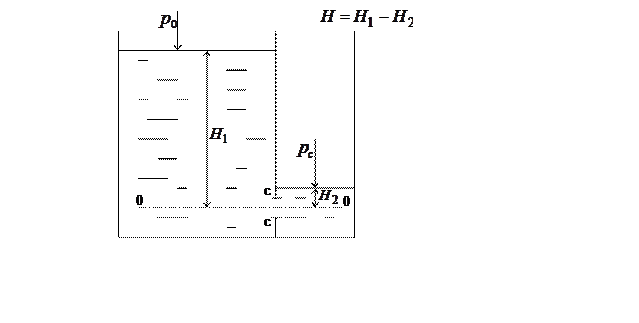
Рис. 1.73. Схема истечения через затопленное отверстие.
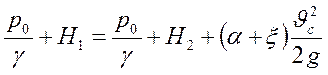 ;
;
или
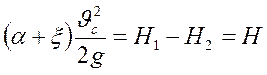 .
.
Следовательно, скорость в сжатом сечении С-С будет равна:
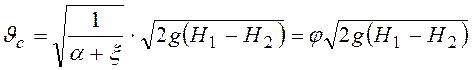 . (122)
. (122)
А расход, при истечении через затопленное отверстие, равен:
![]() . (123)
. (123)
Опытами установлено, что коэффициент расхода ![]() для затопленного и незатопленного
отверстия одинаков.
для затопленного и незатопленного
отверстия одинаков.
Коэффициент расхода ![]() , равный
произведению коэффициента сжатия
, равный
произведению коэффициента сжатия ![]() на
коэффициент скорости
на
коэффициент скорости![]() , зависит также и от типа сжатия
струи.
, зависит также и от типа сжатия
струи.
Для малого отверстия в тонкой стенке ![]() .
.
В случае неполного сжатия струи величина коэффициента ![]() будет больше
будет больше ![]() для
совершения сжатия, то есть,
для
совершения сжатия, то есть,
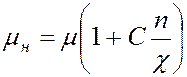 ; (124)
; (124)
где, ![]() - коэффициент: для
круговых отверстий,
- коэффициент: для
круговых отверстий, ![]() = 0,13 , для прямоугольных
отверстий
= 0,13 , для прямоугольных
отверстий ![]() = 0,15;
= 0,15;
![]() -
периметр части отверстии, на которой отсутствует сжатие;
-
периметр части отверстии, на которой отсутствует сжатие;
![]() -
смоченный периметр отверстия.
-
смоченный периметр отверстия.
На коэффициент ![]() влияют
все факторы, которые изменяют
влияют
все факторы, которые изменяют ![]() и
и ![]() .
.
Изменяется ![]() также и от вязкости и
температуры жидкости. Обычно опыты проводились на воде и
также и от вязкости и
температуры жидкости. Обычно опыты проводились на воде и ![]() при изменении
при изменении ![]() =
=![]() (изменение в малых пределах).
(изменение в малых пределах).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.