∆ω→0
На сегодняшний день в гидравлике применяется система измерений СИ, в ней давление равное одному Н/м2 – это один Паскаль.
Но достаточно часто в гидравлике также применяется и система измерений МкГС (особенно при решении задач), в данной системе измерений давление, равное 1 кг/см2 называется технической атмосферой.
Ниже представлены основные соотношения между системами СИ и МкГС.
1Па ≈ 0,00001 ат = 1∙ 10-5 ат.
1 ат = 1 кг/см2 = 105 Па = 100 кПа = 0,1 МПа = 760 мм рт. ст. = 10 м водн. ст.
Гидростатическое давление обладает двумя основными свойствами.
1. Свойство первое (теорема 1). В жидкости, находящейся в состоянии относительного равновесия (покоя) сила воздействия окружающей среды направлена всегда по внутренней нормали к площадке действия жидкости (сила гидростатического давления).
Доказательство от противного (Рис. 1.2).
р – гидростатическое давление. Разложим вектор гидростатического давления на рк и рн, α ≠ 900. рн = р sin α; рк = р cos α , но рк = 0, т. к. покой (по внешней нормали разрыв) рк = р cos α = 0; но р ≠0, то тогда cos α = 0, т. е.
α = 900, следовательно р = рн.
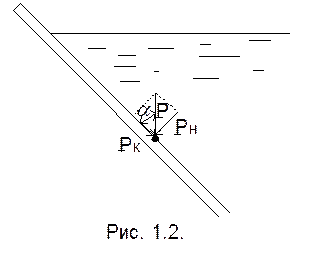
2. Свойство второе (теорема 2). Гидростатическое давление в данной точке не зависит от ориентировки (угла наклона) площадки действия и в различных направлениях одинаково по величине (рх= ру = рz = рn).
1.2.2. Равновесие жидкости, находящейся под действием только
сил тяжести (Основное уравнение гидростатики)
В данном случае из массовых сил на жидкость действует только сила тяжести (рис. 1. 5.) и уравнение приобретает следующий вид:
р =
р0 + γh = р0 + ![]() (10)
(10)
где: р – абсолютное или полное давление в данной точке;
р0 – внешнее поверхностное давление;
рм = γh – избыточное (весовое) или манометрическое давление.
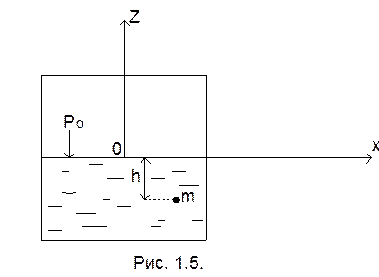
Если сосуд открыт (атмосферное давление и внутри и снаружи), т. е.
р0 = ра, то уравнение принимает следующий вид:
р = ра + γh
Величина превышения абсолютного давления над атмосферным (р – ра) – это избыточное или манометрическое давление.
Основное уравнение гидростатики представляет собой закон распределения давления. Из этого уравнения видно, что с увеличением h , давление p повышается по закону прямой (рис. 1.6).
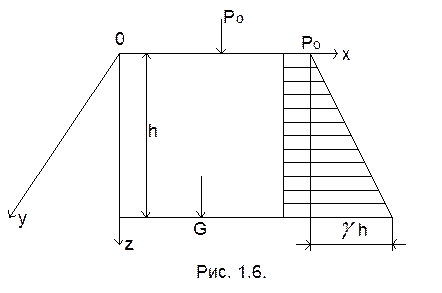
Гидростатическое давление в любой точке жидкости равно давлению над свободной поверхностью, сложенному с весом столба жидкости, основанием которого является единица площади, а высотой – глубина погружения рассматриваемой точки в жидкость.
1.2.3. Пьезометрическая, приведенная высота, вакуум,
напор, удельная потенциальная энергия
Если рассматривать давление жидкости на стенку сосуда в точке, то давление в точке можно выразить с внешней стороны как атмосферное ра, а внутри – как гидростатическое (рис. 1.7.). Стенка испытывает давление, равное разности полного гидростатического давления и атмосферного давления. Это превышение и есть избыточное давление или манометрическое:
р = р0 + γh.
рм = р – ра = р0 + γh – ра. (11)
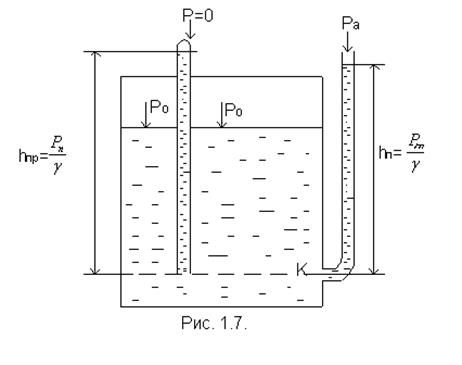
Если р0 = ра, то рм = γh, откуда получаем:
h
= 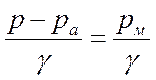 , т. е. по
рисунку
, т. е. по
рисунку
hп = 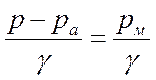 (12)
(12)
где: hп – пьезометрическая или манометрическая высота,
р– полное давление.
Если р = 0, то
hnр =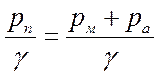 (13)
(13)
где: hnp – приведенная высота;
рп - полное давление;
рм – манометрическое давление;
ра – атмосферное давление.
В гидравлике открытой трубкой (пьезометр) измеряется пьезометрическое давление, а закрытой трубкой измеряется полное давление.
Вакуум – отрицательное манометрическое давление, т. е. превышение атмосферного давления над полным давлением.
Измеряется данное давление вакуумметром или обратным пьезометром (рис. 1.8.).
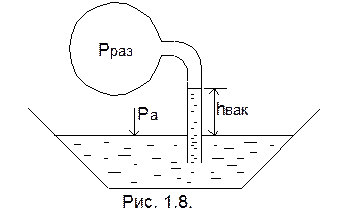
Из рисунка следует, что:
ра = рраз + γhвак (14)
hвак = 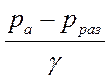 (15)
(15)
Рассмотрим понятие напора (рис.1.9.).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.