Энергетическая сущность уравнения Бернулли состоит в том, что оно выражает закон сохранения энергии в элементарной струйке.
Т.к. сумма трех членов постоянна, то
δЭ1 = δЭ2 = const, т.е.
δЭ
= 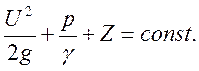 (54)
(54)
Сумма трех членов уравнения (1.52.) есть сумма удельных энергий:
![]() и
и
![]() - удельная кинетическая энергия.
- удельная кинетическая энергия.
![]() и
и ![]() -
удельная потенциальная энергия давления.
-
удельная потенциальная энергия давления.
Z1 и Z2 - удельная потенциальная энергия положения.
Механическая сущность уравнения Бернулли состоит в том, что работа силы тяжести и силы давления равна изменению кинетической энергии в сечениях 2-2 и 1-1 (рис. 1.45.):
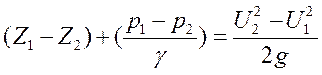 , (55)
, (55)
где: (Z1 – Z2) - работа сил тяжести на единицу веса жидкости;
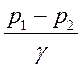 - работа сил
давления на единицу веса жидкости;
- работа сил
давления на единицу веса жидкости;
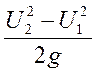 - изменение кинетической энергии на
единицу веса жидкости.
- изменение кинетической энергии на
единицу веса жидкости.
Н![]() - высота напорной
линии (для идеальной жидкости для всех точек одинаковы).
- высота напорной
линии (для идеальной жидкости для всех точек одинаковы).
Нn - высота пьезометрической линии.
Уравнение Бернулли для реальной жидкости.
Распространим уравнение Бернулли для элементарной струйки идеальной жидкости на элементарную струйку реальной жидкости. Это необходимо для решения практических задач. В первую очередь реальная жидкость обладает вязкостью, это обусловливает сопротивление движению, и как следствие, потеря части энергии.
В реальной жидкости удельная энергия по длине струйки уменьшается, переходя частично в тепловую энергию, т.е. получаем:
δЭ1 > δЭ2;
или получаем следующую схему уравнения для струйки реальной жидкости:
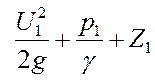 >
> 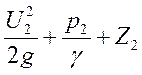 .
.
Т.е. уравнение Бернулли для элементарной струйки реальной жидкости будет иметь следующий вид (рис. 1.47.):
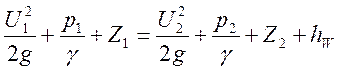 , (56)
, (56)
где: hw = δЭ1 – δЭ2 - потеря энергии по длине струйки.
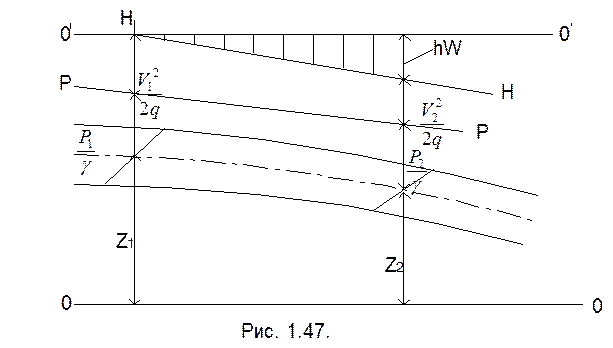
Проинтегрировав уравнение для реальной струйки (предварительно умножив на вес γg), получаем уравнение Бернулли для потока реальной жидкости:
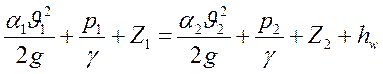 , (57)
, (57)
где: υ1 и υ2 – средняя скорость в рассматриваемых сечениях,
α1, α2 – коэффициент, учитывающий неравномерное распределение скоростей по живому сечению потока.
Практически α1 = α2 = 1,05 ÷ 1,1. При решении задач по гидравлике, не требующих высокой точности, достаточно часто принимают α ≈ 1.
Другими словами α1, α2 – это коэффициент кинетической энергии (коэффициент Кориолиса).
Величина α зависит от распределения скоростей по сечению и ее можно определить по формуле Евреинова:
α = 1 + ![]() ; (58)
; (58)
или формуле Альтшуля:
α = 1 + 2,65 λ; (59)
причем:
С2 = 8g/λ; (60)
где: λ – коэффициент сопротивления трению.
Уравнение Бернулли является важнейшим уравнением гидродинамики, дающим возможность учитывать связь между тремя основными элементами движущейся жидкости: υ, p, Z.
Уравнение справедливо для установившегося или медленно изменяющегося движения.
Уравнение Бернулли можно сформулировать так:
для всех точек данной линии тока:
1. Сумма трех высот – положения, пьезометрической, скоростной – есть величина постоянная.
2. Сумма трех напоров – геометрического, пьезометрического и скоростного есть величина постоянная.
3. Сумма трех удельных энергий – потенциальной энергии положения, давления и кинетической – есть величина постоянная.
1.3.6. Понятие о гидравлическом и пьезометрическом уклонах
Потеря энергии или напора hw представляет собой разность между высотой горизонтальной лини 01 – 01, проведенной через уровень жидкости в трубке Пито в рассматриваемом сечении (рис. 1.48.):
Н1 = 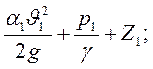 Н2
=
Н2
= 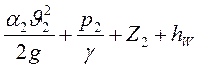 .
.
Гидравлический уклон ![]() - потеря энергии (напора) на
единицу длины потока (Н-Н).
- потеря энергии (напора) на
единицу длины потока (Н-Н).
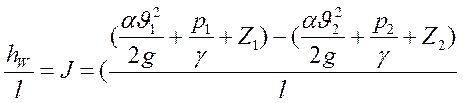 . (61)
. (61)
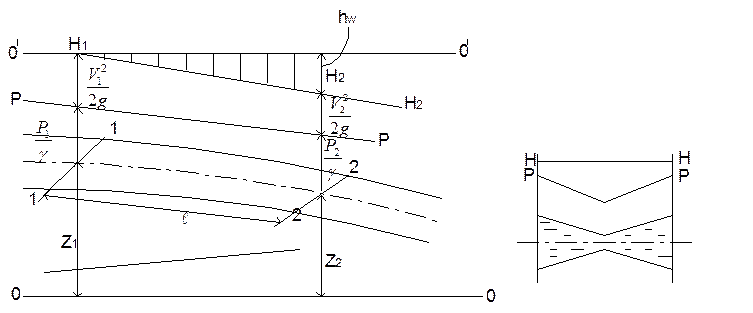 Рис. 1.48. Схема гидравлических и
пьезометрических уклонов.
Рис. 1.48. Схема гидравлических и
пьезометрических уклонов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.