Учебный стенд на базе токарного станка с компьютерным управлением: Учебное пособие, страница 19

где радиус вектор й контрольной точки,

й, базисный сплайн,

радиус вектор, точек кривой, заданной сплайном.

Параметр t изменяется от 0 до 1.

Базисные сплайны будем вычислять с помощью рекуррентных формул, описанных в [1], т.е. с помощью треугольной таблицы. Отличие состоит в том, что, при использовании параметрического вида В-сплайна, носители всех базисных сплайнов будут находиться в промежутке от 0 до 1 параметра t. Никаких отличий в вычислениях нет, однако нам необходимо из последовательности заданных контрольных точек, получить последовательность интервалов  параметра t. Выполним это простым делением интервала  на n-1 равных промежутков, где n – число контрольных точек.

Основные этапы метода аналогичны случаю кубического сплайна, и отличаются лишь расчетными формулами, которые, естественно, выведены для параметрического задания В-сплайна. Поэтому не будем здесь описывать метод подробно.

Реализация сплайновой интерполяции в УЧПУ на базе персонального компьютера позволяет получить следующие положительные результаты:

1)  уменьшение объема управляющих программ;

2)  сокращение времени генерации управляющих программ;

3)  сокращение времени обработки изделия;

4)  улучшение качества обрабатываемой поверхности и, как следствие, исключение операции ручной доводки;

5) уменьшение износа оборудования вследствие улучшения динамики               процесса металлообработки.

Разработанные алгоритмы были реализованы в программном обеспечении систем управления токарным станком и фрезерным станком. Были разработаны форматы новых команд для двумерного и трехмерного случаев. Система команд УЧПУ токарного станка была расширена двумя новыми командами, УЧПУ фрезерного – одной командой. Т.е. была проведена модернизация устройств числового программного управления данных металлорежущих станков. После разработки постпроцессоров для CAD-систем под устройства ЧПУ этих станков, будет возможным генерация управляющих программ без использования процедур аппроксимации линейными отрезками и дугами окружностей.

При разработке был использован
язык ”C”.

Были проведены испытания алгоритмов, подтвердившие теоретические расчеты, и показавшие высокую эффективность описанных выше методов.

В данной статье описан алгоритм воспроизведения устройством числового программного управления криволинейной траектории, заданной с помощью В-сплайна. Рассматривается двумерный случай В-сплайна, применимый в УЧПУ токарного станка.

Алгоритм был реализован в программном обеспечении УЧПУ токарного станка, разработанного на кафедре “Станки и инструмент” ЮУрГУ.

При разработке алгоритма, будем использовать параметрическое представление В-сплайна, описанное в [2]. Это даст возможность впоследствии с минимальными изменениями перенести алгоритм на трехмерный случай для фрезерного станка. Сплайн в этом случае определяется векторным уравнений:

    (1)  

где радиус вектор й контрольной точки,

й, базисный сплайн,

радиус вектор, точек кривой, заданной сплайном.

Параметр t изменяется от 0 до 1.

Базисные сплайны будем вычислять с помощью рекуррентных формул, описанных в [1], т.е. с помощью треугольной таблицы. Отличие состоит в том, что, при использовании параметрического вида В-сплайна, носители всех базисных сплайнов будут находиться в промежутке от 0 до 1 параметра t. Никаких отличий в вычислениях нет, однако нам необходимо из последовательности заданных контрольных точек, получить последовательность интервалов  параметра t. Выполним это простым делением интервала  на n-1 равных промежутков, где n – число контрольных точек.

В-сплайн для точек [x1,y1],[x2,y2],[x3,y3] показан на рис. 1.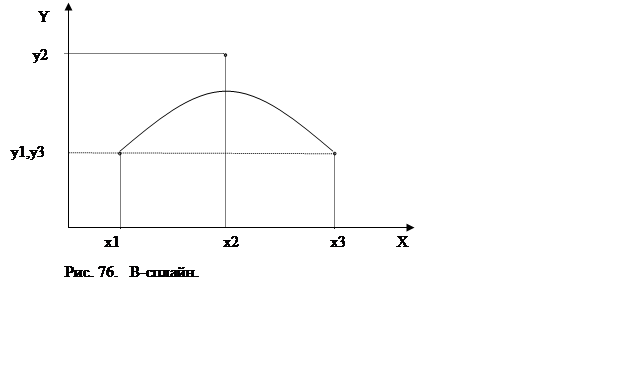

Cначала попытаемся использовать вектор движения, параллельный, касательной к траектории. Для его нахождения необходимо найти производные x и y по t. Дифференцирование В-сплайнов подробно описано в [1].

Можно записать следующие формулы, для

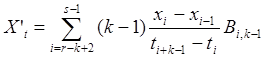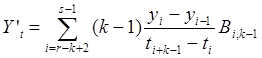 на

 на

т.е. для нахождения производных, необходимо вычислить все не равные 0 на  базисные сплайны, порядок которых на единицу меньше, т.е.