Учебный стенд на базе токарного станка с компьютерным управлением: Учебное пособие, страница 17

          Длина отрезков аппроксимации дуги зависит от величины приращения угла dA и равна линейному расстоянию dL между точками, принадлежащими дуге окружности, угловое расстояние между которыми равно величине приращения угла. 

          В основном цикле алгоритма сначала происходит увеличение начального угла на величину углового приращения и производится расчёт следую­щей точки на дуге окружности. Далее вычисляются приращения координат между этими двумя точками. В следующем шаге происходит вызов процеду­ры линейной интерполяции (line) и перемещение суппорта по прямой в конечную точку текущего отрезка. После завершения перемещения производится сохранение значений текущих координат и цикл повторяется. Основ­ной цикл продолжается до тех пор, пока значение начального угла не станет больше или равно значению конечного угла (A_n ³ A_k). Блок схема алгоритма круговой интерполяции представлена для первой четверти окружности. Все вычисления координат производятся для первой четверти, направ­ления движения задаются путём установки знаков перемещений в зависимости от четверти системы координат, в которой происходит движение.

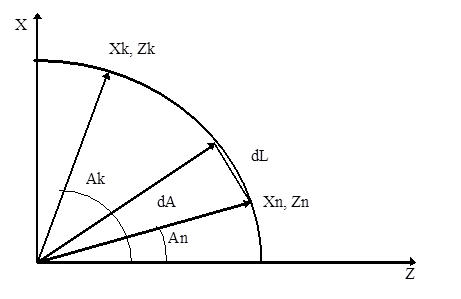
Рис. 71. Круговая интерполяция

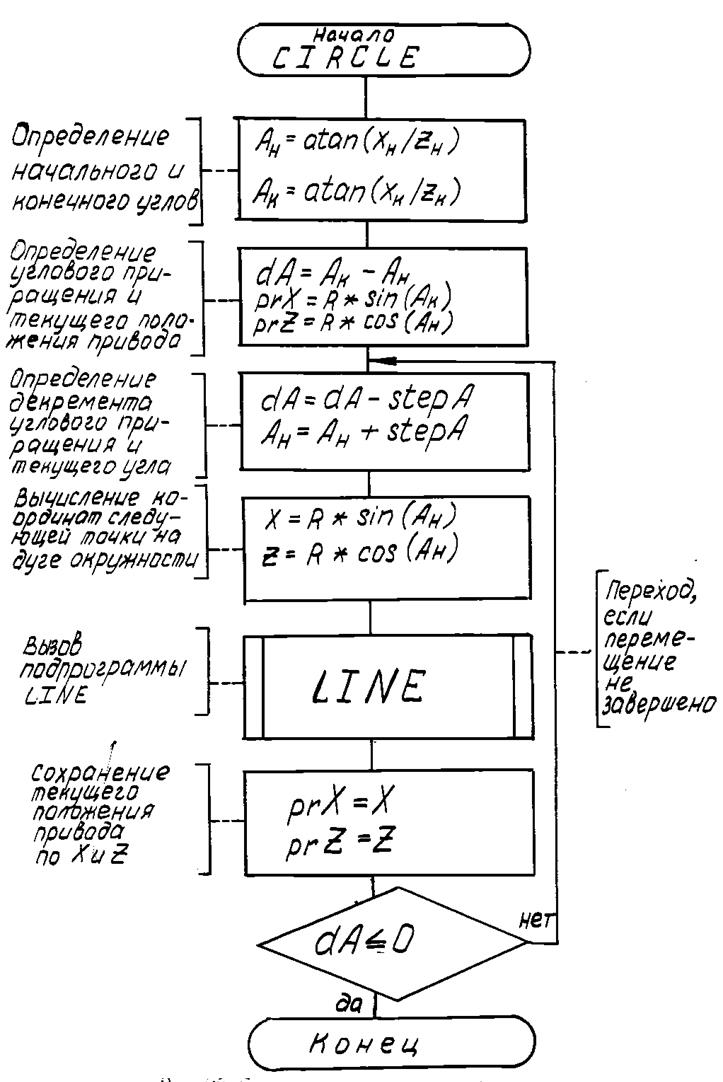
Рис. 72. Схема алгоритма круговой интерполяции

6.2.3. Сплайновая интерполяция

Суть поставленной задачи сводится к разработке алгоритмов движения рабочего инструмента станка с заданной скоростью по траектории заданной в виде сплайна (интерполяционного кубического или В-сплайна). Для токарного станка достаточно двумерного случая, так как резец двигается в одной плоскости, тогда как для фрезерного станка необходимо было разработать алгоритм движения инструмента по траектории заданной трехмерной кривой (в нашем случае - сплайном).

B-сплайны - это оптимальное средство для определения рельефных поверхностей, вследствие чего они активно используются в САПР. В-сплайны присутствуют в трехмерной модели практически любой детали. Поэтому их главное использование в УЧПУ - это служить интерфейсом для CAD систем. При их наличии в интерполяторе, возможна генерация управляющей программы без использования аппроксимации. В-сплайны позволяют решать большую часть задач связанных с воспроизведением инструментом станка различных кривых. Однако, в УЧПУ также необходимо наличие средства для воспроизведения траектории по заданным точкам лежащим прямо на кривой. Для этого следует использовать какой-либо другой вид сплайна, который позволяет строить кривые проходящие через заданные узлы. Наиболее подходящими для решения данной задачи
видятся кубические сплайны.

Кубический сплайн задается с помощью выражения:

                                (1)

коэффициенты которого, определяются с помощью таблицы разделенных разностей, для каждого интервала между точками разрыва .

Метод, с помощью которого инструмент станка движется по такой траектории, основан на определении составляющих вектора контурной скорости по координатам X и Y (Здесь и далее будем применять обозначения координатных осей принятых в математической литературе. В связи со станком оси обычно обозначают X,Z).

Т.е. вектор движения V, по модулю равный заданной скорости  разлагается на составляющие по осям, численные значения которых  передаются соответствующим приводам, отвечающим за движение по каждой координате.

Основная расчетная задача состоит в определении такого вектора движения, чтобы инструмент двигался по траектории с минимальной погрешностью.

Самым простым было бы движение по вектору, параллельному касательной к траектории в той точке, в которой в данный момент находится инструмент (рис. 1).

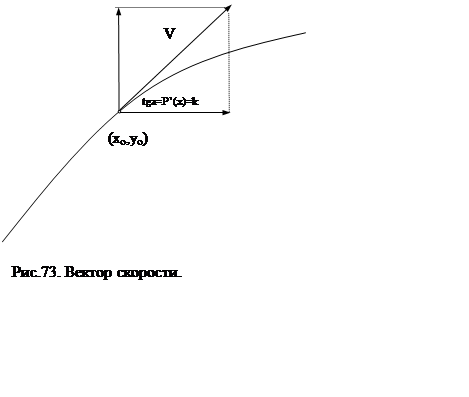Из (1) можно получить выражение для расчета производной кубического сплайна на интервале :

                                                            (2)

Коэффициенты рассчитаем с помощью таблицы разделенных разностей по формулам:

 (3)                            

Теперь, зная , мы можем найти составляющие вектора скорости по координатным осям

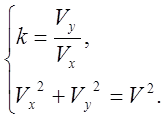
отсюда получаем:

 далее

и находим составляющие вектора скорости:

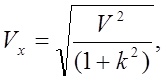
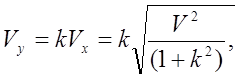
где