Учебный стенд на базе токарного станка с компьютерным управлением: Учебное пособие, страница 16

          - представление необходимой пользователю информации в удобном для него виде.

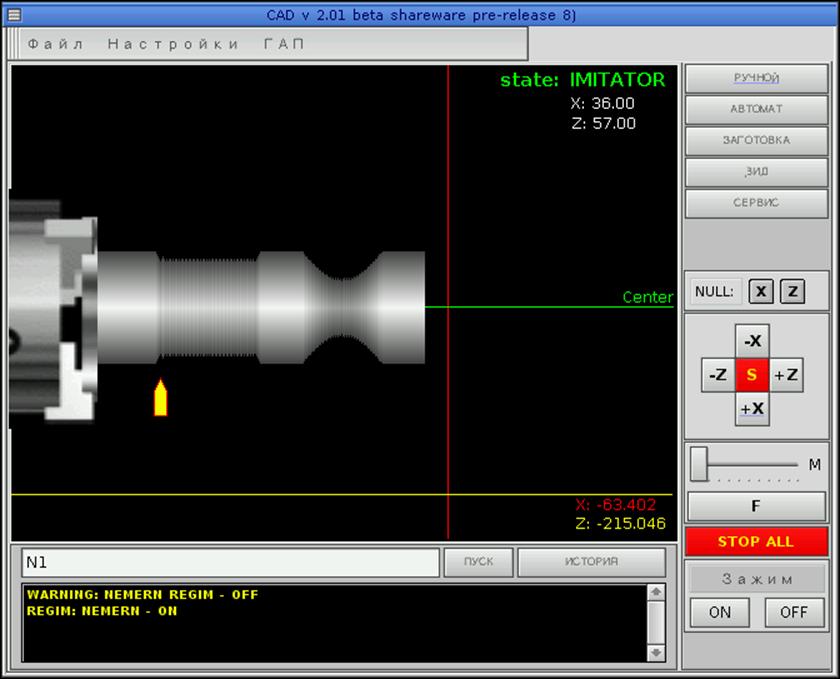
Рис.67.

Рис.68.

6.2. Решение задач интерполяции

          Вычислительное содержание задачи формообразования, сводящееся по существу к воспроизведению заданных траекторий включает: движение по заданной траектории (интерполяция), поддержка постоянной контурной скорости.

          Задачи интерполяции траектории являются основной составляющей частью управления движением и занимают по времени не менее 35%-40%  общего цикла оперативного управления. 

6.2.1. Линейная интерполяция

          Блок схема алгоритма линейной интерполяции показана на рис. 26. 

          В основе применяемого алгоритма линейной интерполяции лежит определение составляющей вектора контурной скорости по координатам Х и Z (рис. 65).

          Составляющая вектора скорости подачи V_х­ по координате Х рассчитываются по формуле:

;

где   V_k    - контурная скорость подачи;

     dx, dz - приращения перемещений.

          Составляющая вектора по координате Z рассчитываются по формуле:

;

          После определения составляющих вектора контурной скорости происходит чтение и сохранение текущего состояния датчиков обратной связи по положению приводов подач (pred_d_i) (рис. 66). Начинается основной цикл алгоритма, он длится до тех пор пока заданные приращения вдоль координат Х и Z (dX и dZ) не станут равными 0 (dX = 0, dZ = 0).

          Основной цикл алгоритма состоит из двух частей. Первая содержит обработку данных, относящихся к приводу Х, вторая - к приводу Z. Обработка данных ведётся последовательно - сначала по координате Х, затем по координате Z. В блоке обработки данных по координате Х сначала происходит сравнение текущего и предыдущего показаний датчика положения. Если показания не изменились, то происходит переход к обработке данных по Z. Если показания датчика изменились, то производится проверка флага завершения перемещения по координате Х, если флаг установлен, то - переход к обработке данных по Z. Если флаг не установлен, то производится вычисление смещения суппорта по координате Х и уменьшение заданного перемещения на эту величину. Далее производится аналогичная обработка данных по координате Z.

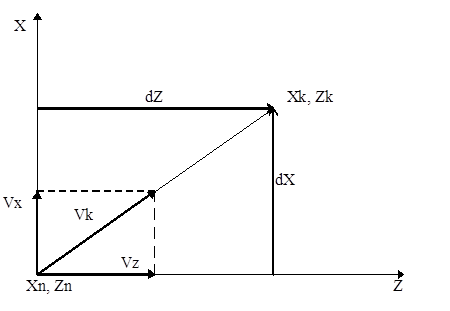
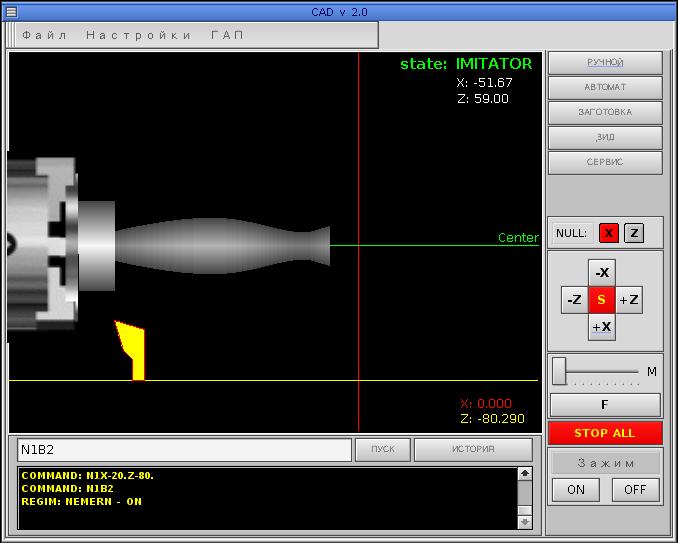
 Рис. 69. Линейная интерполяция

          После обработки данных по Х и по Z следует блок коррекции скорости. В соответствие с текущими значениями заданных перемещений производится вычисление составляющих контурной скорости по выражениям  V_x и V_z. 

          Передача данных от программы к интерфейсу управления осущест­вляется через порты компьютера. Данные (управляющий код или управляющее слово) записываются в соответствующий порт.

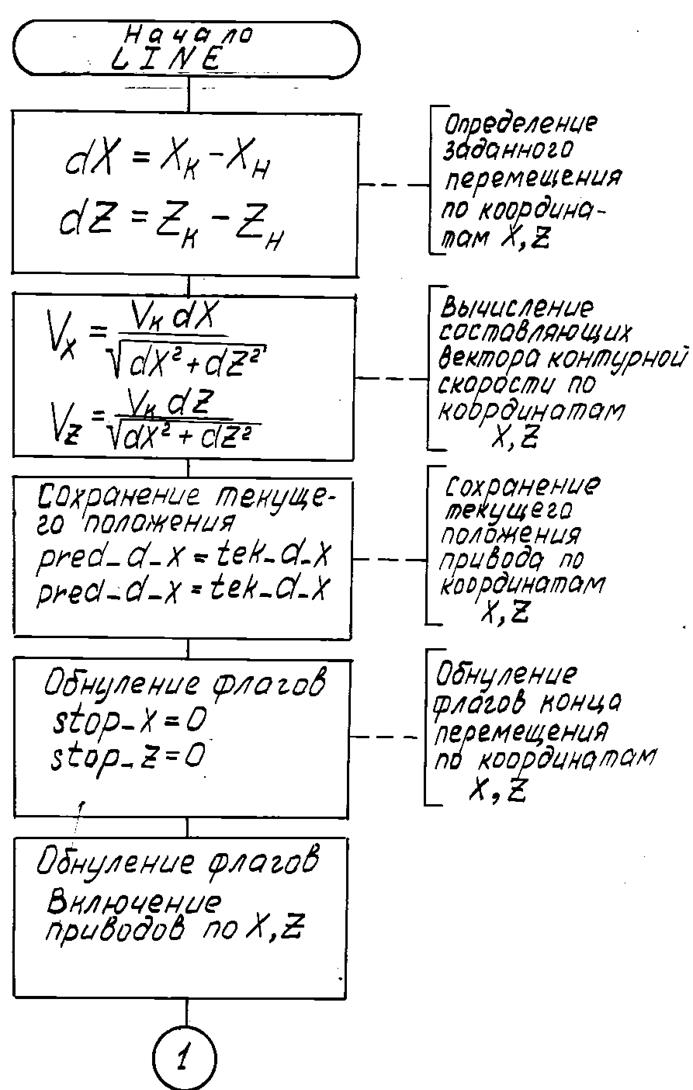
Рис. 70. Алгоритм линейной интерполяции

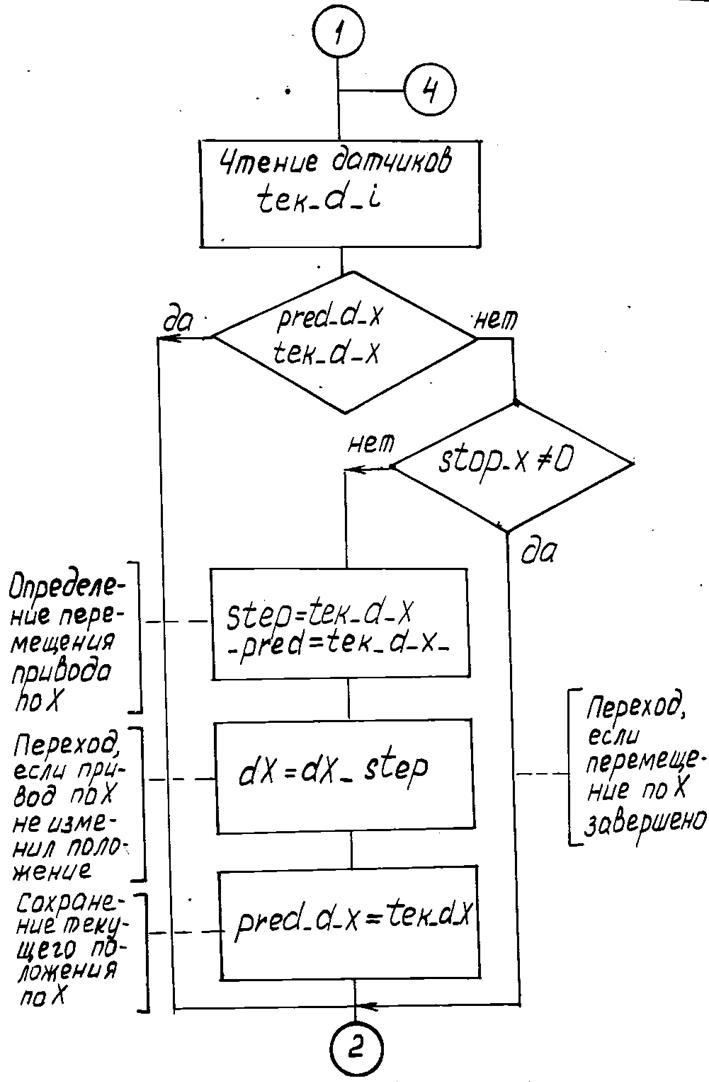
Рис.70. Алгоритм линейной интерполяции (продолжение)

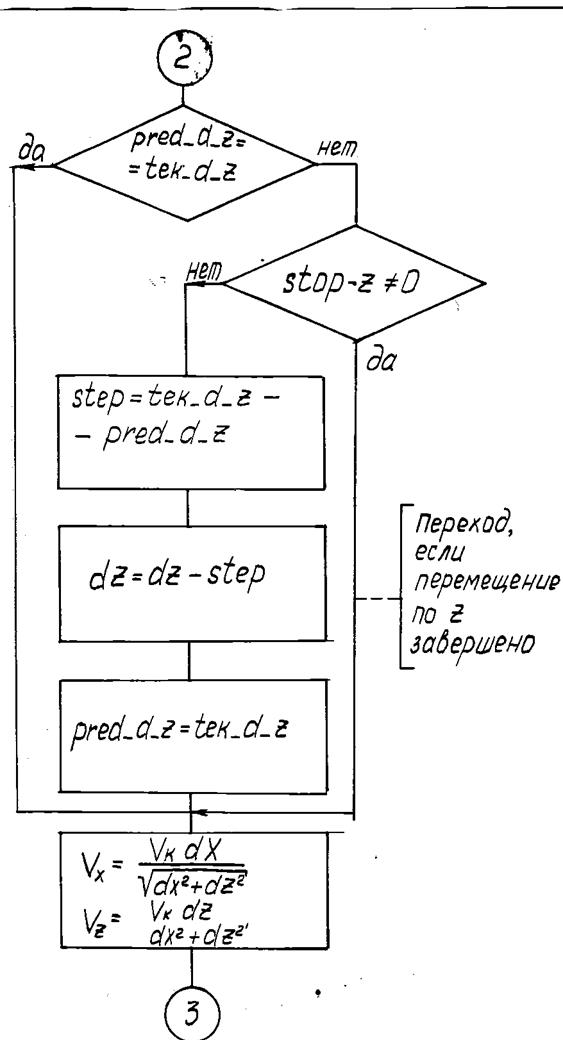
Рис. 70. Схема алгоритма линейной интерполяции (продолжение)

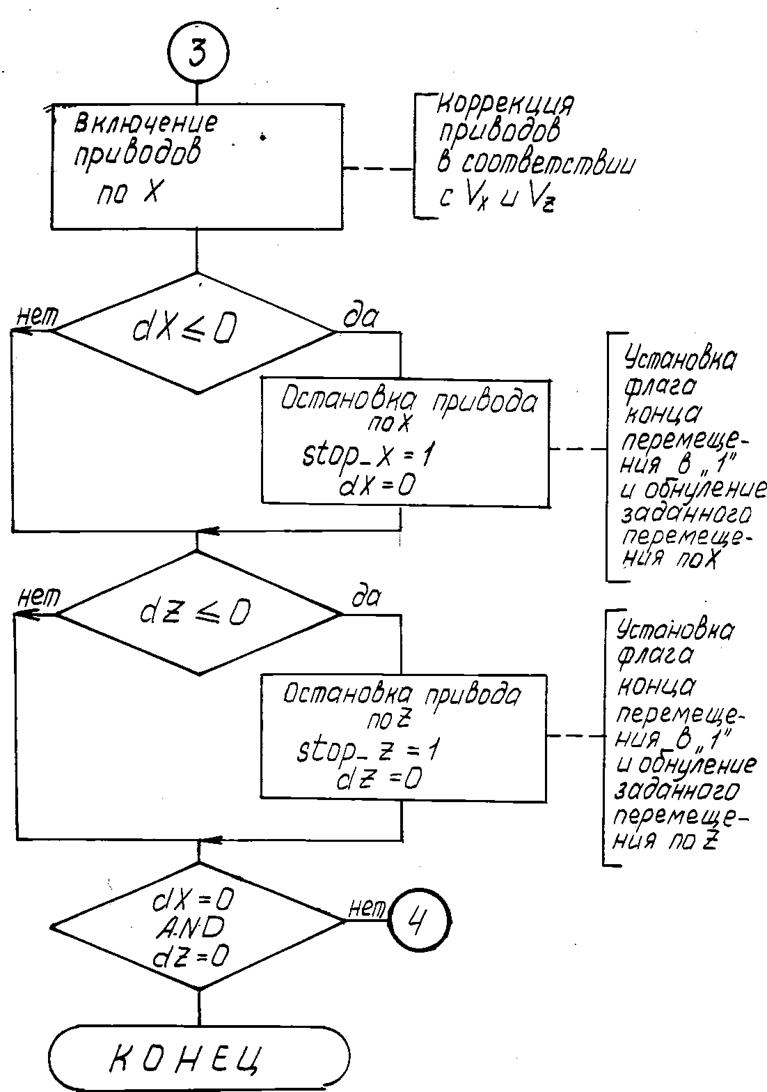
Рис.70. Алгоритм линейной интерполяции (окончание)

          Преобразование кода скорости подачи в код производится по следующей формуле:

V_cod = (N_pod × 255)/150;

где V_cod - кодированное значение скорости подачи;

     N_pod - требуемая скорость подачи в мм/мин.

          Требуемая скорость главного движения, преобразованная в код, передаётся в формирователь импульсов путём записи этого кода в соответст­вую­щий порт.

          Следующим шагом в работе алгоритма является проверка на завершение заданного перемещения вдоль координат. Если перемещение по Х или по Z завершено, то происходит установка соответствующего флага в “1” и обнуление заданного перемещения вдоль этой координаты.

6.2.2. Круговая интерполяция

          Алгоритм круговой интерполяции (рис. 28) построен по принципу аппроксимации дуги окружности линейными отрезками (рис. 29). На этапе подготовки данных определяются начальный А_n и конечный A_к углы дуги окружности. Определение этих углов производится по формулам:

A_n = arctan(Xstart/Zstart);

где Xstart, Zstart - координаты начальной точки дуги окружности;

A_k = arctan(Xendt/Zend);

где Xend, Zend - координаты начальной точки дуги окружности.