Учебный стенд на базе токарного станка с компьютерным управлением: Учебное пособие, страница 18

При движении с небольшой по модулю скоростью данный метод вполне приемлем, так как перемещение инструмента происходит на небольшое расстояние, которое столь мало, что траекторию, заданную сплайном, можно считать прямой. Инструмент практически не сходит с заданной кривой и погрешность невелика. Однако при повышении скорости обработки, погрешность будет увеличиваться, поэтому необходимо разработать меры по коррекции траектории.

Будем считать, что рабочий инструмент сошел с заданной траектории вследствие высокой скорости подачи, зазоров в кинематической схеме привода подачи или каких-то неучтенных факторов. Рассчитанный вектор движения в этом случае еще больше увеличивает погрешность. Моделирование показало, что движение инструмента по траектории в этом случае выглядит следующим образом (рис. 2):

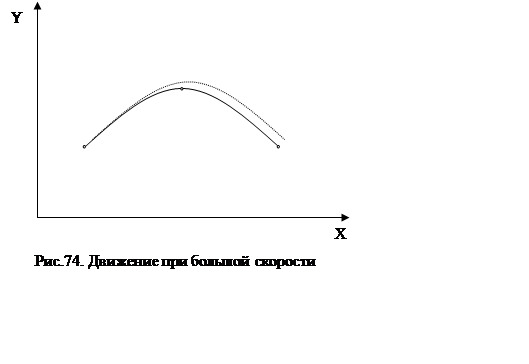Для коррекции движения будем изменять составляющие вектора скорости как показано на рис.3.

Т.е. рассчитаем вектор смещения с траектории по оси OY,  и новый вектор скорости вычислим, как разность вектора V, и вектора смещения.

Таким образом, новый вектор движения будет следующим:

Для того, чтобы найти вектор смещения, необходимо знать текущие координаты инструмента, а также координату Y точки траектории, в которой должен находиться инструмент при значении координаты по оси OX, равном x_o. Т.е. необходимо вычислить значение сплайна при

С учетом этого скорректированный вектор скорости:

При вычислении коэффициентов сплайна, свободные параметры  определяются из системы линейных алгебраических уравнений:

где     

В [1] и [11] предлагается решать систему с помощью метода Гаусса, число операций в котором 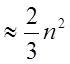. Однако для этой системы мы получаем трехдиагональную матрицу коэффициентов с диагональным преобладанием. Поэтому имеется возможность использовать метод прогонки, так как выполняется условие устойчивости вычислений. Метод прогонки в данном случае будет более эффективным, так как число операций в нем  Это сократит время вычислений и соответственно уменьшит погрешность, так как управляющее воздействие будет происходить с большей частотой.

Следует заметить, что для таких расчетов, необходимо знать на каком отрезке, кусочно-заданного полинома (сплайна) в данный момент находится инструмент, для того, чтобы правильно вычислить коэффициенты сплайна, или правильно выбрать их, если расчет проводится перед началом движения.

Моделирование показало, что при таком методе коррекции существенно уменьшается погрешность движения по траектории.

Как уже упоминалось ранее, существует несколько способов задания граничных условий для кубических сплайнов. Естественно, что при применении данного метода, абсолютно безразлично, какой из способов используется. Способ выбирает инженер при проектировании детали в CAD – системе, поэтому в УЧПУ следует реализовать поддержку нескольких из них. Способ задания граничных условий через первые производные в крайних точках, является обязательным к реализации.

В заключение надо отметить, что использованное здесь представление интерполяционного кубического сплайна в явном виде, а не в параметрическом, не позволяет задавать замкнутые или самопересекающиеся траектории для инструмента станка. Однако это не является недостатком в случае токарного станка, для которого этот метод и разрабатывался. Для инструмента токарного станка, в отличие от фрезерного, нет необходимости в движениях по подобным траекториям, поэтому  методы, основанные на таком представлении кубического сплайна, могут достаточно широко применяться.

Далее кратко расмотрим особенности воспроизведения траектории заданной с помощью B-сплайна, который, как известно, является основой технологии NURBS.

При разработке алгоритма, использовано параметрическое представление В-сплайна, описанное в [7]. Это дает возможность с минимальными изменениями перенести алгоритм на трехмерный случай для фрезерного станка. Сплайн в этом случае определяется векторным уравнений: