Позднее возникла проблема построения и представления этих вопросов так, чтобы инициатива исследования исходила от самого ученика. Этого мы постарались добиться при помощи изменения характера формулируемых вопросов (внушая уверенность ученику в его возможностях).
Возникала проблема вариантов ответа ученика на поставленный вопрос, т.е. каким образом выстроить дальнейший материал так, чтобы он не зависел от характера ответа на вопрос. Такой вопрос преобразовывался в один или даже два других наводящих вопроса. Рассмотрим пример. Ставится вопрос: верно ли утверждение: Если диагонали четырехугольника равны, то четырехугольник прямоугольный.
Сразу возникает желание предложить: если ДА, то докажи, если НЕТ, то приведи контрпример. Мы хотели избежать такой поляризации ответов.
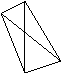
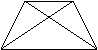
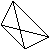
Мы предложили ученику нарисовать несколько разных пар равных пересекающихся отрезков, а потом соединить их концы (рис.3.1). Полученные им четырехугольники дают ему основания для выполнения задания.
 |
|||||
 |
 |
||||
Рис.3.1
При проведении анализа предметного материала был частично исследован четырехугольник с самопересечением. Результаты этого исследования нас не удовлетворили. Получить «интересные» факты, т.е. обнаружить свойства не удалось, а свойства присущие основной фигуре – трапеции, не выполняются. Так например, углы при боковой стороне трапеции равны 180°, в случае же четырехугольника с самопересечением данное свойство не выполняется. С другой стороны можно было бы выделить следующее свойство такой фигуры: углы при боковой стороне равны.

Рис.3.2
Но данное свойство принадлежит не самой фигуре, а является свойством любой секущей, поэтому мы не стали его выделять. Свойство средней линии трапеции (она равна полусумме оснований) также не выполняется. Это просто наблюдать в том случае, когда точка самопересечения находится близко к средней линии.
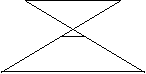 |
Рис.3.3
По причинам того, что задачей при исследовании четырехугольников является изучение их свойств, четырехугольник с самопересечением не был включен нами в основное изучение курса. У него не были обнаружены «интересные» для изучения свойства. Данный четырехугольник был вынесен в блок для дополнительного, необязательного для всех изучения, «задание для любознательных».
Процесс работы школьника с учебной тетрадью видоизменяется по ходу разворачивания материала. Но этот ход задается логикой восхождения от абстрактного к конкретному, которая выражается в переходе от общего к особым случаям.
В тетради происходит движение от рода к видам четырехугольников. Движение имеет вид последовательного рассмотрения всех возможных отношений между элементами четырехугольника. Первый параграф тетради посвящен рассмотрению общих отношений равенства, перпендикулярности и параллельности. Именно в такой последовательности и проводится «учебное» исследование, т.к. отношение равенства задает множество пробных вариантов не представляющих интереса для изучения свойств. Отношение перпендикулярности задает лишь три четырехугольника два из которых являются особыми. Отношение параллельности имеет один особый случай – трапецию.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.