Учебная тетрадь по теме «Четырехугольник» как средство реализации решения учебной проблемы, страница 23

Если нужна помощь, обратись к учебнику – 17 стр.

Обоснуй  каждое из утверждений.

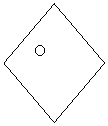            В

                                 АОВ=АОД=СОВ=СОД, т.к. 

А                       С    АВ=ВС=СД=ДА, по

                                ОВ=ОД  и  АО=ОС

  Сделай вывод и сформулируй теорему о свойстве  

Д                    диагоналей ромба.

рис.2.17   

Вспомни различия свойств и признаков объектов. Зная  свойство, сформулируй признак диагоналей ромба.

 

Будет ли верным утверждение: если диагонали четырехугольника пересекаются под прямым углом и являются биссектрисами всех углов, то этот четырехугольник - ромб?

Посмотри на рис.2.18: 

Он удовлетворяет условию диагоналей?

Соотношения каких элементов недостает для того,                                  рис.2.18

чтобы  данный четырехугольник стал ромбом?

Докажи утверждение о том, что диагонали ромба являются  биссектрисами углов.

Сделай рисунок.

                                                        Рис.2.19

Воспользуйся свойством равнобедренных треугольников.

 

Выдели равные треугольники и сделай вывод.

 

Рассмотрим ромб, у которого все  углы прямые. Его ты знаешь уже давно. Вспомни как он называется и дай его определение.

 

 На основе изученных в предыдущих пунктах фигур сформулируй следующие определения.

Квадратом называется четырехугольник, у которого

Квадратом называется трапеция, у которой

Квадратом называется прямоугольник, у которого