Учебная тетрадь по теме «Четырехугольник» как средство реализации решения учебной проблемы, страница 17

                                                                             стороне

с равными противолежащими углами

Сколько всего разных по форме трапеций ты получил?

Сделай вывод о влиянии одних соотношений четырехугольника на другие.

 

Нарисуй произвольную трапецию

                                                        Рис.1.19

Продолжи до прямых основания трапеции и одну из ее  боковых сторон. Отметь на рис.1.16 равные углы. Почему эти углы равны?

 

Сделай вывод о углах трапеции при боковой стороне.

 

Обратное утверждение  к тому, что дал ты, будет звучать следующим образом: если углы четырехугольника при боковой стороне равны 180º, то этот четырехугольник трапеция.

С другой стороны верно и отрицание этого утверждения: если углы при боковой стороне четырехугольной фигуры не равны 180º, то данная фигура не является простой трапецией.

 

Задание для любознательных!!!

В данном параграфе ты узнал свойства простой трапеции, а так же то, что трапеция является четырехугольником с двумя параллельными сторонами. Но ты знаешь, что четырехугольник  с самопересечением так же имеет две параллельные стороны (рис.1.20).

 

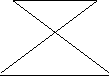Рис.1.20

Выполняются ли доказанные выше свойства для такого четырехугольника (рис.1.20)? Или, может быть, ты найдешь  новые свойства, присущие только ему. Проведи исследование свойств четырехугольника с самопересечением в тетрадке для творческих работ.

Сделай вывод о свойствах четырехугольника  с самопересечением, у которого две параллельных стороны.

 

§2.2 Особые четырехугольники

2.2.1 Особые четырехугольники с отношением параллельности

Мы считаем, что задача, которую тебе предстоит далее решить в данном пункте, связана с ограничением четырехугольника на два элемента.

Так ли это? Далее тебе предстоит ответить.

В предыдущем параграфе, ты изучил фигуру называемую трапецией. Давай наложим ограничения на нее так, чтобы получить какие-нибудь интересные формы, т.е. исследуем ее.

Изобрази трапецию, у которой боковые стороны равны и не параллельны.

                                                        Рис.2.1

Такая трапеция называется равнобокой.

Посмотри на углы прилежащие к основанию. Что ты можешь о них сказать?

 

Теперь изобрази трапецию, у которой углы при основании равны.

                                                        Рис.2.2

Чтоты заметил?