На рисунке 26,б приведена модель тракта ПП – РС на цепи участковой диспетчерской ТТС. Поскольку абонент промпункта вызывает диспетчера голосом, то tтех =0.
На рисунке 26,в дана модель тракта ПП – ПП на цепи постанционной связи.
Более наглядными являются деревья графов составляющих времени передачи информации по трактам связи на цепях участковых ТТС, приведенные на рисунке 29.
Как видно из рисунка 29,а из-за наличия или отсутствия той или иной составляющей имеется возможность установления тракта связи РС – ПП на диспетчерской цепи разными путями аibi. Число состояний системы N определяется:
N=n·m, (5)
где n– число входов системы, m – число выходов системы.
Поскольку n=1и m =8, то существует 8 вариантов установления тракта связи РС – ПП.
Для трактов ПП – РС (рисунок 29,б) n=2 и m=8, следовательно, существует N=2·8=16 вариантов установления тракта.
Для трактов ПП – ПП на цепях постанционной связи (рисунок 29,в) n=4 и m=16, следовательно, существует N=4·16=64 варианта установления тракта.
Вероятность прохождения тракта связи по той или иной ветви деревьев графов, изображенных на рисунке 29, можно представить, как произведение вероятностей существования составляющих времени занятия цепи:
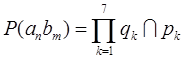 . (6)
. (6)
В соответствии с выражением (6) для дерева, изображенного на рисунке 29,а, получим:
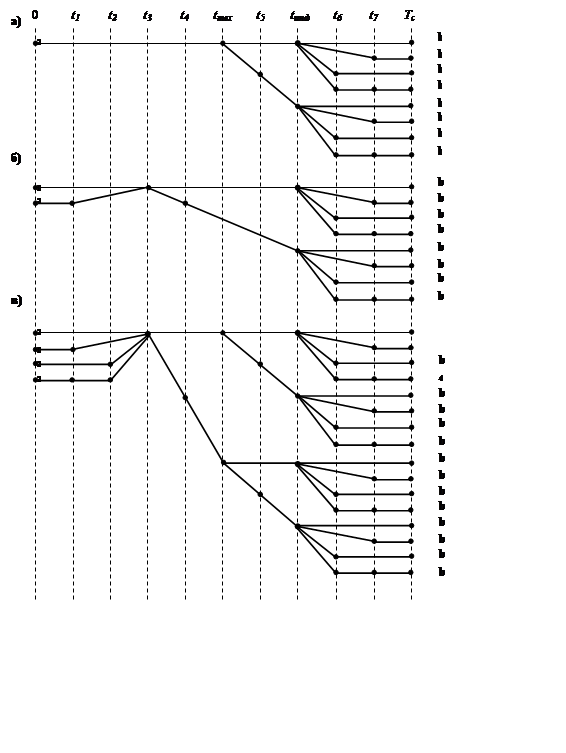
Рисунок 29– Деревья графов составляющих времени установления трактов связи на цепях участковых ТТС
![]() P(a1b1)=q1 •
q2 • q3 • q4 • q5 •
q6 • q7
P(a1b1)=q1 •
q2 • q3 • q4 • q5 •
q6 • q7
P(a1b2)= q1 • q2 • q3 • q4 • q5 • q6 • p7
P(a1b3)= q1 • q2 • q3 • q4 • q5 • p6 • q7
![]() P(a1b4)=
q1 • q2 • q3 • q4 •
q5 • p6 • p7
P(a1b4)=
q1 • q2 • q3 • q4 •
q5 • p6 • p7
P(a1b5)= q1 • q2 • q3 • q4 • p5 • q6 • q7
P(a1b6)= q1 • q2 • q3 • q4 • p5 • q6 • p7
P(a1b7)= q1 • q2 • q3 • q4 • p5 • p6 • q7
P(a1b8)= q1 • q2 • q3 • q4 • p5 • p6 • p7
Для дерева, изображенного на рисунке 29,б, имеем:
P(a1b1)= q1 • q2 • p3 • q4 • q5 • q6 • q7
![]() P(a1b2)=
q1 • q2 • p3 • q4 •
q5 • q6 • p7
P(a1b2)=
q1 • q2 • p3 • q4 •
q5 • q6 • p7
P(a1b3)= q1 • q2 • p3 • q4 • q5 • p6 • q7
P(a1b4)= q1 • q2 • p3 • q4 • q5 • p6 • p7
P(a1b5)= q1 • q2 • p3 • p4 • q5 • q6 • q7
P(a1b6)= q1 • q2 • p3 • p4 • q5 • q6 • p7
P(a1b7)= q1 • q2 • p3 • p4 • q5 • p6 • q7
![]() P(a1b8)=
q1 • q2 • p3 • p4 •
q5 • p6 • p7
P(a1b8)=
q1 • q2 • p3 • p4 •
q5 • p6 • p7
P(a2b1)= p1 • q2 • p3 • q4 • q5 • q6 • q7
P(a2b2)= p1 • q2 • p3 • q4 • q5 • q6 • p7
P(a2b3)= p1 • q2 • p3 • q4 • q5 • p6 • q7
P(a2b4)= p1 • q2 • p3 • q4 • q5 • p6 • p7
P(a2b5)= p1 • q2 • p3 • p4 • q5 • q6 • q7
P(a2b6)= p1 • q2 • p3 • p4 • q5 • q6 • p7
P(a2b7)= p1 • q2 • p3 • p4 • q5 • p6 • q7
P(a2b8)= p1 • q2 • p3 • p4 • q5 • p6 • p7
И для дерева, изображенного на рисунке 29, в, получим:
![]() P(a1b1)= q1 •
q2 • p3 • q4 • q5 •
q6 • q7
P(a1b1)= q1 •
q2 • p3 • q4 • q5 •
q6 • q7
P(a1b2)= q1 • q2 • p3 • q4 • q5 • q6 • p7
P(a1b3)= q1 • q2 • p3 • q4 • q5 • p6 • q7
………………………………………
P(a1b10)= q1 • q2 • p3 • p4 • q5 • q6 • p7
P(a1b11)= q1 • q2 • p3 • p4 • q5 • p6 • q7
P(a1b12)= q1 • q2 • p3 • p4 • q5 • p6 • p7
P(a1b13)= q1 • q2 • p3 • p4 • p5 • q6 • q7
P(a1b14)= q1 • q2 • p3 • p4 • p5 • q6 • p7
![]() P(a1b15)=
q1 • q2 • p3 • p4 •
p5 • p6 • q7
P(a1b15)=
q1 • q2 • p3 • p4 •
p5 • p6 • q7
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.