



















































1. Некоторые примеры экономических задач, приводящих к модели
линейного программирования (ЛП)
Пример 1. Задача об использовании ресурсов.
При производстве двух видов
продукции (![]() ) используются четыре вида ресурсов:
) используются четыре вида ресурсов: ![]() Затраты ресурсов каждого вида на
производство одной единицы продукции каждого вида, имеющиеся запасы ресурсов и
доходы от реализации одной единицы продукции заданы в таблице 1.
Затраты ресурсов каждого вида на
производство одной единицы продукции каждого вида, имеющиеся запасы ресурсов и
доходы от реализации одной единицы продукции заданы в таблице 1.
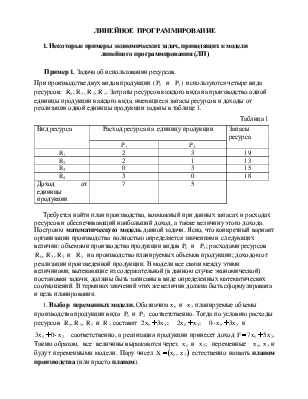
Таблица 1
|
Вид ресурса |
Расход ресурса на единицу продукции |
Запасы ресурса |
|
|
P1 |
P2 |
||
|
R1 |
2 |
3 |
19 |
|
R2 |
2 |
1 |
13 |
|
R3 |
0 |
3 |
15 |
|
R4 |
3 |
0 |
18 |
|
Доход от единицы продукции |
7 |
5 |
|
Требуется найти план
производства, возможный при данных запасах и расходах ресурсов и обеспечивающий
наибольший доход, а также величину этого дохода. Построим математическую
модель данной задачи. Ясно, что конкретный вариант организации
производства полностью определяется значениями следующих величин: объемами
производства продукции видов ![]() ; расходами ресурсов
; расходами ресурсов ![]() на производство планируемых объемов
продукции; доходом от реализации произведенной продукции. В модели все связи
между этими величинами, вытекающие из содержательной (в данном случае
экономической) постановки задачи, должны быть записаны в виде определенных
математических соотношений. В терминах значений этих же величин должна быть
сформулирована и цель планирования.
на производство планируемых объемов
продукции; доходом от реализации произведенной продукции. В модели все связи
между этими величинами, вытекающие из содержательной (в данном случае
экономической) постановки задачи, должны быть записаны в виде определенных
математических соотношений. В терминах значений этих же величин должна быть
сформулирована и цель планирования.
1. Выбор переменных
модели. Обозначим ![]() планируемые объемы производства
продукции вида
планируемые объемы производства
продукции вида ![]() соответственно. Тогда по
условию расходы ресурсов
соответственно. Тогда по
условию расходы ресурсов ![]() составят
составят ![]() и
и
![]() соответственно, а реализация продукции
принесет доход
соответственно, а реализация продукции
принесет доход ![]() . Таким образом, все величины
выражаются через
. Таким образом, все величины
выражаются через ![]() переменные
переменные ![]() и будут переменными модели. Пару чисел
и будут переменными модели. Пару чисел ![]() естественно назвать планом производства
(или просто планом).
естественно назвать планом производства
(или просто планом).
2. Целевая функция. Целью планирования является максимизация величины
![]() (целевой
функции).
(целевой
функции).
3. Ограничения на переменные. Возможность осуществления плана ![]() эквивалентна выполнению следующих условий:
расходы ресурсов
эквивалентна выполнению следующих условий:
расходы ресурсов ![]()
![]()
![]()
![]() не
превосходят соответствующих запасов 19, 13,
15, 18; объемы производств
не
превосходят соответствующих запасов 19, 13,
15, 18; объемы производств ![]() - неотрицательные
числа.
- неотрицательные
числа.
Все изложенное в 1 - 3 позволяет записать математическую модель рассматриваемой задачи в виде
![]() (1)
(1)
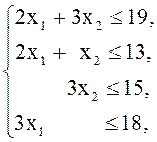 (2)
(2)
![]() .
(3)
.
(3)
Более подробно задача (1) –
(3) понимается следующим образом: среди всех пар чисел ![]() (планов задачи), удовлетворяющих
ограничениям (2) и (3), найти такую, для которой функция
(планов задачи), удовлетворяющих
ограничениям (2) и (3), найти такую, для которой функция ![]() принимает наибольшее значение.
принимает наибольшее значение.
Для n видов продукции и m видов ресурсов математическая модель задачи о ресурсах имеет вид
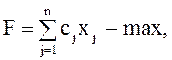 (4)
(4)
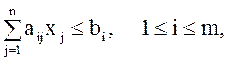 (5)
(5)
![]() (6)
(6)
где ![]() - расход i-го ресурса на
производство единицы j - й продукции; bi - запас
- расход i-го ресурса на
производство единицы j - й продукции; bi - запас
i-го ресурса; сj - доход от реализации единицы j - й продукции. В плане задачи
![]() компонента
xj означает планируемый объем производства j-й
продукции. Матрицу
компонента
xj означает планируемый объем производства j-й
продукции. Матрицу ![]() принято называть технологической
матрицей задачи о ресурсах.
принято называть технологической
матрицей задачи о ресурсах.
Пример 2. Задача о диете (витаминах,
смесях). Имеется n видов продуктов питания ![]() содержащих
питательные вещества (витамины)
содержащих
питательные вещества (витамины) ![]() Известно, что единица
продукта
Известно, что единица
продукта ![]() имеет стоимость
имеет стоимость ![]() и
содержит
и
содержит ![]() единиц витаминов
единиц витаминов ![]() необходимый
минимум витамина
необходимый
минимум витамина ![]() составляет
составляет ![]() единиц в день,
единиц в день, ![]() Требуется
составить дневной рацион питания минимальной стоимости, содержащий необходимое
количество каждого витамина.
Требуется
составить дневной рацион питания минимальной стоимости, содержащий необходимое
количество каждого витамина.
Дневной рацион
характеризуется набором из n чисел ![]() где
где ![]() - количество продукта
- количество продукта ![]() в рационе, и математическая модель задачи
имеет вид
в рационе, и математическая модель задачи
имеет вид
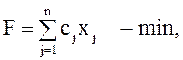 (7)
(7)
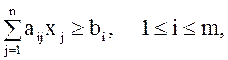 (8)
(8)
![]() (9)
(9)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.