Линейное программирование. Некоторые примеры экономических задач, приводящих к модели линейного программирования. Геометрическая интерпретация и графическое решение задачи ЛП, страница 8

     Выше  намеренно ничего не говорилось  о способах вычисления элементов

 симплексной таблицы по исходным данным  , так как это фактически не понадобится в дальнейшем. Понадобится лишь процедура  нахождения по уже имеющейся симплексной таблице другой, базис которой отличается от базиса исходной всего одной переменной.

                                                                                                                            Таблица 2

     Пусть в таблице 2   Элемент    называется  разрешающим, содержащие   его  строка     (включая  )  и  столбец      (включая )  называются

разрешающими. Разрешающей строке соответствует уравнение

                                     ,

 которое  можно записать  в виде

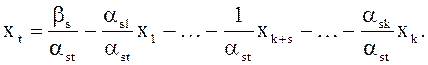                                                               (27)

Во всех остальных уравнениях системы (25), (26) подставим вместо     выражение этой  переменной через переменные  из  равенства (27). В результате получим  систему уравнений, эквивалентную системе (25), (26), а, значит, и системе (17), (18). Новой записи системы соответствует симплексная таблица 3, базис которой получается из базиса таблицы 2 заменой   на   .

                                                                                                                             Таблица 3

Здесь и  в дальнейшем надписи «базисные переменные», «свободные переменные», «1» и знаки «=» в первом столбце опускаются.                                                                                                                                                                                                                                                                                         

     Таблица 3 называется симплексным преобразованием  таблицы 2 с разрешающим элементом и получается из таблицы 2 по следующим  правилам:

   1) переменные   меняются местами;

   2) разрешающий элемент заменяется обратной величиной  ;

   3) остальные элементы разрешающей строки делятся на  разрешающий элемент;

   4) остальные элементы разрешающего столбца делятся на разрешающий элемент и  меняют знак  на противоположный   

   5) каждый из оставшихся  элементов  u  (в том числе в строке F и столбце свободных членов), не принадлежащиx  ни разрешающей строке, ни разрешающему столбцу, заменяется на  , который вычисляется по правилу прямоугольника,

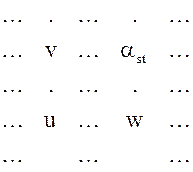
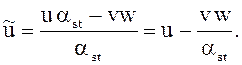
Здесь v – элемент  на  пересечении  разрешающей  строки  со  столбцом, содержа-

щим u; w - элемент на пересечении разрешающего столбца со строкой, содержащей u.