Линейное программирование. Некоторые примеры экономических задач, приводящих к модели линейного программирования. Геометрическая интерпретация и графическое решение задачи ЛП, страница 5

     Чтобы найти оптимальный план    задачи, выберем произвольную точку М внутри области допустимых планов, проведем через нее прямую, перпендикулярную вектору   (на рис. 1 изображена пунктиром) и будем перемещать эту прямую параллельно самой себе в направлении    до тех пор, пока перемещаемая прямая будет содержать хотя бы одну точку области допустимых планов. В «крайнем» возможном положении  (рис. 1) линия уровня пройдет через точку  С, в которой и достигается    среди всех допустимых планов  . Координаты точки С находятся из системы

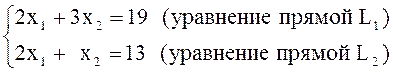
Отсюда  

Задача ЛП  (1) - (3) является моделью задачи о ресурсах с исходными данными, представленными в таблице 1. Найденное выше решение задачи  (1) - (3) означает, что при данных условиях производства 50 является наибольшим из возможных значений дохода. Такой доход может быть  достигнут только тогда, когда производятся 5 единиц продукции   и 3 единицы продукции   

     Аналогично разобранному  примеру можно дать геометрическую интерпретацию любой задачи ЛП с  двумя  переменными и ограничениями-неравенствами,

                                                                                    (23)

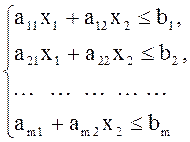                                                                                                      (24)

(требования неотрицательности   считаем включенными в (24) в виде  ).  Область    допустимых   планов   задачи (23) - (24) получается пересечением  m  полуплоскостей, задаваемых неравенствами (24), и представляет собой (в зависимости от расположения этих полуплоскостей) либо пустое множество (рис. 2а), либо единственную точку (рис. 2б), либо выпуклый многоугольник (рис. 2в), либо выпуклую многоугольную область (рис. 2г).

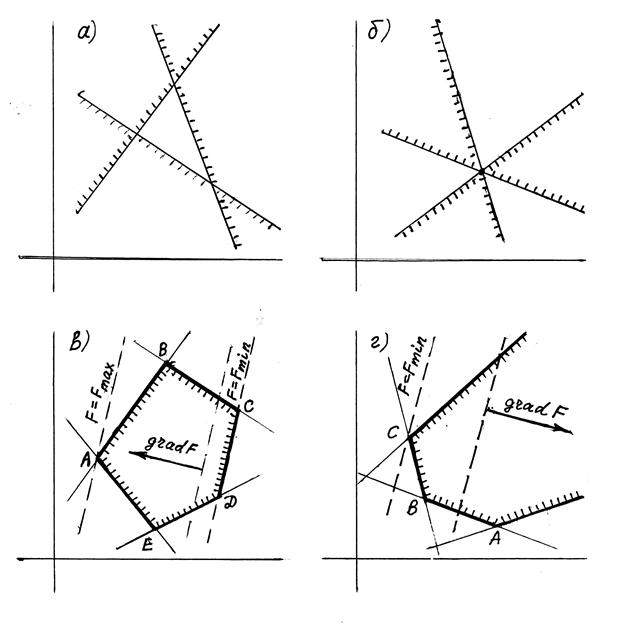
Рис. 2

     В первом случае задача ЛП не имеет решения, так как у нее нет допустимых планов; во втором случае единственный допустимый план является оптимальным. В остальных случаях оптимальные планы  находятся с помощью линий уровня целевой функции (23), пересекающих область допустимых планов. Все эти линии – прямые, перпендикулярные вектору   Оптимальные планы задачи на    лежат на прямой, «крайней» в направлении вектора  а задачи на   - на прямой, «крайней» в направлении противоположного вектора   В зависимости от вида области допустимых планов и направления    возможны следующие случаи:

     а) задача ЛП (23) - (24) имеет единственный оптимальный план  в вершине  многоугольника или многоугольной области ( на рис. 2в  достигается в точке А,   на рис. 2г– в точке С);

     б) множество оптимальных планов бесконечно и состоит из всех точек некоторого  ребра на границе области допустимых планов  ( на рис. 2в достигается во всех точках ребра CD, включая  вершины C и D), или в случае неограниченной многоугольной области, из всех точек граничного  луча  (постройте графическое изображение соответствующей задачи  ЛП самостоятельно);

     в) множество оптимальных планов  пусто   из-за  неограниченности  целевой функции в области допустимых планов ( на рис. 2г).

   Для задачи ЛП в стандартной форме (14)-(16) с тремя переменными неравенство   определяет одно их двух полупространств, на которые делит все пространство  плоскость    Изображением области допустимых планов будет выпуклый многогранник или неограниченная выпуклая многогранная область. Целевая  функция   принимает заданное значение  d  на плоскости   (поверхность уровня). «Крайняя» в направлении вектора   из поверхностей уровня, имеющих непустое пересечение с областью допустимых планов, содержит все оптимальные планы. Множество всех оптимальных планов геометрически представляет собой или грань (возможно бесконечную), или  ребро (луч), или единственную вершину на границе области допустимых планов. Задача  ЛП не имеет оптимальных планов, если ее область допустимых планов либо пуста, либо не ограничена в направлении вектора  .