![]() В строке F таблицы
В строке F таблицы ![]() есть отрицательные
элементы, (-3) – наибольший из них по модулю, поэтому столбец
есть отрицательные
элементы, (-3) – наибольший из них по модулю, поэтому столбец ![]() разрешающий (выделен). В разрешающем столбце
разрешающий (выделен). В разрешающем столбце
![]() есть положительные элементы (в данном
случае все). Вычисляем симплексные отношения 12/4, 8/4, 8/4 (столбец
есть положительные элементы (в данном
случае все). Вычисляем симплексные отношения 12/4, 8/4, 8/4 (столбец
![]() ). Здесь оказались две строки
). Здесь оказались две строки ![]() с минимальным симплексным отношением
с минимальным симплексным отношением ![]() , выбираем в качестве разрешающей одну из
них, например
, выбираем в качестве разрешающей одну из
них, например ![]() (выделена). Элемент 4 на пересечении
строки
(выделена). Элемент 4 на пересечении
строки ![]() и столбца
и столбца ![]() разрешающий.
Далее выполняем симплексное преобразование таблицы
разрешающий.
Далее выполняем симплексное преобразование таблицы ![]() по
правилам 1) - 5) и переходим к
по
правилам 1) - 5) и переходим к ![]() меняем местами
меняем местами ![]() заменяем разрешающий элемент 4 на 1/4; остальные
элементы разрешающей строки, 1 и 8, делим на 4; остальные элементы
разрешающего столбца, 4, 4 и (-3), делим на (-4); все оставшиеся элементы, не
принадлежащие ни строке
заменяем разрешающий элемент 4 на 1/4; остальные
элементы разрешающей строки, 1 и 8, делим на 4; остальные элементы
разрешающего столбца, 4, 4 и (-3), делим на (-4); все оставшиеся элементы, не
принадлежащие ни строке ![]() ни столбцу
ни столбцу ![]() пересчитываем по правилу четырехугольника.
Например, -2 в строке F заменяем на
пересчитываем по правилу четырехугольника.
Например, -2 в строке F заменяем на ![]() 3 в
столбце
3 в
столбце ![]() – на
– на ![]() Теперь
таблица
Теперь
таблица ![]() и опорный план
и опорный план ![]() текущие,
текущие,
![]() и все операции начиная с шага 2
повторяются с таблицей
и все операции начиная с шага 2
повторяются с таблицей ![]() В строке F таблицы
В строке F таблицы
![]() еще есть отрицательный элемент
еще есть отрицательный элемент ![]() в разрешающем столбце
в разрешающем столбце ![]() есть положительные элементы 2 и 1/4.
После вычисления симплексных отношений ( почему в строке
есть положительные элементы 2 и 1/4.
После вычисления симплексных отношений ( почему в строке ![]() вместо отношения стоит прочерк?) и выбора
разрешающего элемента 2 надо выполнить симплексное преобразование таблицы
вместо отношения стоит прочерк?) и выбора
разрешающего элемента 2 надо выполнить симплексное преобразование таблицы ![]()
т.
е. перейти к ![]() При этом целесообразно начать
вычисления с элементов строки F: если они окажутся неотрицательными (в данном случае
так и будет: получатся
При этом целесообразно начать
вычисления с элементов строки F: если они окажутся неотрицательными (в данном случае
так и будет: получатся ![]() ), то
), то ![]() будет заключительной, ей
соответствует оптимальный опорный план. Чтобы выписать этот план и
будет заключительной, ей
соответствует оптимальный опорный план. Чтобы выписать этот план и ![]() , нужен только столбец свободных членов
таблицы, «внутренние» элементы
, нужен только столбец свободных членов
таблицы, «внутренние» элементы ![]() можно не вычислять.
Итак, в данной задаче
можно не вычислять.
Итак, в данной задаче ![]() единственный
оптимальный план и
единственный
оптимальный план и ![]()
При втором варианте выбора разрешающей строки в ![]() вместо
вместо
![]() получается другая цепочка таблиц:
получается другая цепочка таблиц: ![]() где
где
![]()
![]()
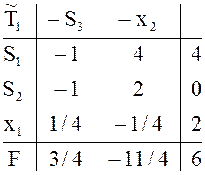
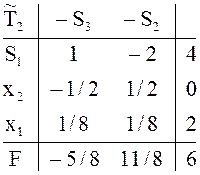
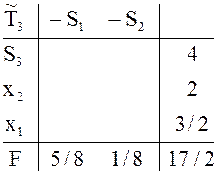
Здесь и в дальнейшем столбцы симплексных отношений опущены и сразу выделены
разрешающие элементы. Вторая цепочка тоже приводит к оптимальному плану
(конечно, тому же самому ![]() ведь он
единственный!). Заметим, что в каждом из опорных планов
ведь он
единственный!). Заметим, что в каждом из опорных планов ![]() таблиц
таблиц ![]() есть базисное переменное с нулевым значением (см.
столбцы свободных членов) - задача вырождена. Более того,
есть базисное переменное с нулевым значением (см.
столбцы свободных членов) - задача вырождена. Более того, ![]() хотя таблицы
хотя таблицы ![]() различные.
различные.
Пример 10 показывает, что при применении симплекс-метода к вырожденной задаче
нескольким последовательным таблицам может соответствовать один и тот же
опорный план (![]() во второй цепочке).
Оказывается, что в других (более сложных) вырожденных задачах возможна
следующая ситуация: нескольким таблицам соответствует один и тот же опорный
план и на некотором шаге очередная из этих таблиц повторяет одну из предыдущих
– происходит зацикливание. В теории ЛП разработаны различные варианты
уточнения основного алгоритма симплекс-метода, позволяющие избежать
зацикливания, но при решении практических задач они применяются очень редко,
так как их использование сильно замедляет вычислительный процесс, а вероятность
зацикливания ничтожно мала.
во второй цепочке).
Оказывается, что в других (более сложных) вырожденных задачах возможна
следующая ситуация: нескольким таблицам соответствует один и тот же опорный
план и на некотором шаге очередная из этих таблиц повторяет одну из предыдущих
– происходит зацикливание. В теории ЛП разработаны различные варианты
уточнения основного алгоритма симплекс-метода, позволяющие избежать
зацикливания, но при решении практических задач они применяются очень редко,
так как их использование сильно замедляет вычислительный процесс, а вероятность
зацикливания ничтожно мала.
В заключение приведем пример решения задачи о ресурсах с помощью симплекс-метода.
Пример 11. В таблице 4 представлены исходные данные задачи о ресурсах:
|
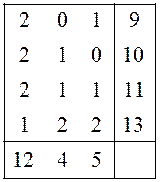
Решение. Обозначим ![]() планируемые объемы
производства по видам продукции. Математической моделью будет задача ЛП в
стандартной (записана слева) или канонической (справа) форме:
планируемые объемы
производства по видам продукции. Математической моделью будет задача ЛП в
стандартной (записана слева) или канонической (справа) форме:
![]()
![]()
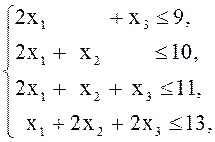
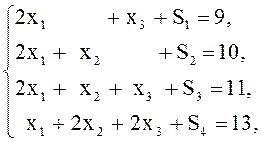
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.