Сведение задачи о
ресурсах (4) - (6) к каноническому виду
требуют только введения балансовых переменных ![]() и
приводит к модели
и
приводит к модели
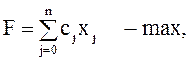 (20)
(20)
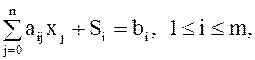 (21)
(21)
![]() (22)
(22)
При этом балансовые
переменные ![]() имеют очевидный экономический смысл:
имеют очевидный экономический смысл:
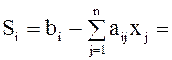 (запас i-го ресурса) -
(расход i-го ресурса)=(остаток i-го ресурса),
(запас i-го ресурса) -
(расход i-го ресурса)=(остаток i-го ресурса), ![]()
Модель (7) - (9) задачи о диете имеет «почти» стандартную форму. Надо только умножить неравенства (8) на (-1) и заменить минимизацию F на максимизацию
(-F). Модель (10) -
(13) транспортной задачи принимает канонический вид после замены ![]() - min на (-F) -
max.
- min на (-F) -
max.
Упражнения
1. Привести модель (7) - (9) задачи о диете к каноническому виду. Какой содержательный смысл имеют балансовые переменные?
2. Привести к канонической форме следующие задачи ЛП:
a) ![]() б)
б) ![]()
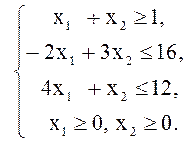
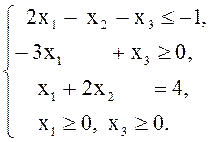
в) ![]() г)
г) ![]()
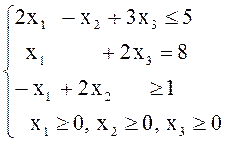
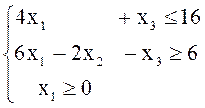
3. Привести к стандартной форме следующие задачи ЛП:
a) ![]() б)
б)
![]()
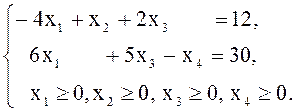
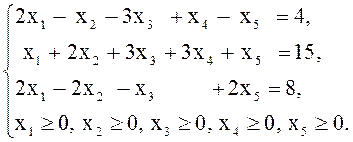
в)
![]() г)
г) ![]()
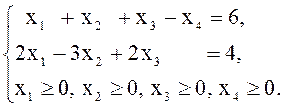
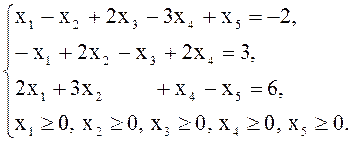
3. Геометрическая интерпретация и графическое решение задачи ЛП
При изучении задач ЛП важную роль играет возможность геометрического описания множества всех допустимых планов и целевой функции рассматриваемой задачи. И хотя в общем случае это приводит к сложным построениям в многомерном пространстве, все главные особенности задач ЛП можно увидеть уже на простых примерах.
Пример 6. Рассмотрим задачу (1) - (3) из примера 1.
![]()
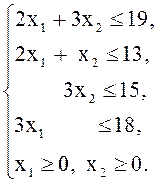
Каждому плану ![]() задачи соответствует вполне
определенная точка на плоскости
задачи соответствует вполне
определенная точка на плоскости ![]() именно точка с
координатами
именно точка с
координатами ![]() Допустимым планам соответствуют
точки, координаты которых удовлетворяют всем ограничениям-неравенствам.
Решениями первого неравенства
Допустимым планам соответствуют
точки, координаты которых удовлетворяют всем ограничениям-неравенствам.
Решениями первого неравенства ![]() будут все решения
уравнения
будут все решения
уравнения ![]() и все решения неравенства
и все решения неравенства ![]() Как известно из аналитической геометрии,
линейное уравнение
Как известно из аналитической геометрии,
линейное уравнение ![]() задает на плоскости определенную
прямую
задает на плоскости определенную
прямую ![]() Эту прямую можно построить, например, по
двум точкам ее пересечения с осями координат:
Эту прямую можно построить, например, по
двум точкам ее пересечения с осями координат: ![]() .
Прямая
.
Прямая ![]() делит всю плоскость на две полуплоскости:
для точек одной из них выполнено неравенство
делит всю плоскость на две полуплоскости:
для точек одной из них выполнено неравенство ![]() для
точек другой – неравенство
для
точек другой – неравенство ![]() Начало координат
Начало координат ![]() расположено в первой из этих
полуплоскостей, так как
расположено в первой из этих
полуплоскостей, так как ![]()
Из
сказанного выше ясно, что геометрически множество всех планов, удовлетворяющих
неравенству ![]() представляет собой ту из
полуплоскостей с граничной прямой
представляет собой ту из
полуплоскостей с граничной прямой ![]() , которая содержит
начало координат (сама прямая
, которая содержит
начало координат (сама прямая ![]() включается в эту
полуплоскость). Аналогично строятся граничные прямые и полуплоскости,
соответствующие остальным ограничениям-неравенствам. Например, для третьего
неравенства
включается в эту
полуплоскость). Аналогично строятся граничные прямые и полуплоскости,
соответствующие остальным ограничениям-неравенствам. Например, для третьего
неравенства ![]() граничной будет горизонтальная
(параллельная оси Ох1) прямая
граничной будет горизонтальная
(параллельная оси Ох1) прямая ![]() а
«решения» этого неравенства – все точки на прямой
а
«решения» этого неравенства – все точки на прямой ![]() и ниже
нее. Граничными прямыми для неравенств
и ниже
нее. Граничными прямыми для неравенств ![]() являются
координатные оси
являются
координатные оси ![]() соответственно.
соответственно.
|
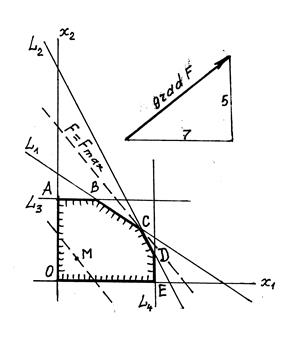
Все линии семейства (при
различных d) – прямые, перпендикулярные одному и тому же вектору
![]() с координатами
с координатами ![]() =
=![]() и, следовательно, параллельные между
собой. Во всех точках прямой
и, следовательно, параллельные между
собой. Во всех точках прямой ![]() функция F,
по определению, принимает одно и то же значение d; сдвиг этой
прямой параллельно самой себе в направлении вектора
функция F,
по определению, принимает одно и то же значение d; сдвиг этой
прямой параллельно самой себе в направлении вектора ![]() дает
линию уровня
дает
линию уровня ![]() где
где ![]() так как
градиент функции указывает направление ее наискорейшего возрастания.
так как
градиент функции указывает направление ее наискорейшего возрастания.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.