Математика \ Высшая математика

Линейное программирование. Некоторые примеры экономических задач, приводящих к модели линейного программирования. Геометрическая интерпретация и графическое решение задачи ЛП, страница 9

При любом выборе базиса все планы, удовлетворяющие (18), в том числе все допустимые планы, можно получить, придавая свободным переменным произвольные значения и вычисляя значения базисных переменных по их выражениям через свободные. Планы, которые получаются указанным способом при нулевых значениях свободных переменных, называются базисными. Симплексной табли-це 2 (уравнениям (25), (26)) соответствует базисный план в котором при этом Базисный план будет допустимым тогда и только тогда, когда значения всех базисных переменных ( т. е. свободные члены симплексной таблицы) неотрицательны. Допустимые базисные планы называются опорными. Симплексные таблицы с неотрицательными свободными членами называются допустимыми.

Предположим, что таблица 2 допустима и, кроме того, все коэффициенты в строке F неотрицательны ( может быть и отрицательным). Тогда для любого допустимого плана будет выполнено неравенство (учесть, что )

Это означает, что - наибольшее из значений целевой функции на допустимых планах, т. е. опорный план является оптимальным. Если все коэффициенты положительны, т. е. среди них нет не только отрицательных чисел, но и нулей, опорный план будет единственным оптимальным планом задачи (17)-(19). Действительно, в этом случае для любого допустимого плана среди чисел а значит и среди произведений есть хотя бы одно положительное, т. е. выполнено строгое неравенство .

Требование неотрицательности (положительности) элементов строки F (не считая свободного члена) называется условием оптимальности (строгой оптимальности) симплексной таблицы. Доказанное выше утверждение можно сформулировать следующим образом.

Критерий оптимальности. Если симплексная таблица одновременно допустима и удовлетворяет условию оптимальности, соответствующий ей опорный план является оптимальным. При выполнении условия строгой оптимальности таблицы это единственный оптимальный план задачи ЛП.

Рассмотрим на примерах, как можно использовать критерий оптимальности и введенные выше понятия и определения для решения задач ЛП.

Пример 7. Приведем задачу (1)-(3), уже решенную графически в примере 6, к канонической форме. Выражая балансовые переменные через получим

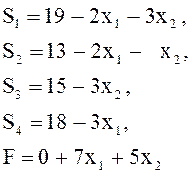
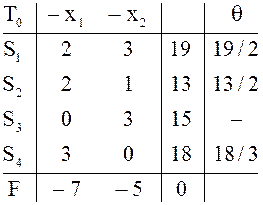
Здесь требования неотрицательности опущены; форма записи уравнений означает, что - базисные, - свободные. Справа от уравнений представлена соответствующая симплексная таблица, в левом верхнем углу–обозначение этой таблицы. В выделены столбец и строка , а также добавлен стол- бец .В дальнейшем выяснится, для чего это сделано. В допустимых планах значения свободных переменных неотрицательны и однозначно определяют значения всех остальных переменных, включая F. При получаем опорный план (ему соответствует вершина О(0 ,0), рис.1) и Чтобы «улучшить» план (увеличить значение F), надо заменить хотя бы одно из нулевых значений на положительное. В любом случае F возрастет, т. к. коэффициенты 7 и 5 (-7 и -5 в таблице Т₀) при переменных положительны. Будем увеличивать только (выделяем столбец , оставляя (почему не наоборот?). При С ростом значения убывают (см. положительные элементы в выделенном столбце ) и обращаются в нуль при соответственно (см. столбец в прочерк в строке соответствует тому, что при и возрастании значение не убывает и остается неотрицательным). При все базисные переменные неотрицательны и соответствующие планы задачи ЛП допустимы; при первой из базисных обращается в нуль переменная (- минимальное из отношений в столбце , выделяем строку ); при планы задачи становятся недопустимыми. Значению отвечает , , т. е. допустимый план и