Линейное программирование. Некоторые примеры экономических задач, приводящих к модели линейного программирования. Геометрическая интерпретация и графическое решение задачи ЛП, страница 10

После упрощений,                                             

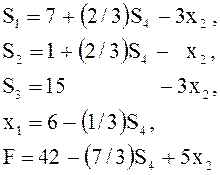
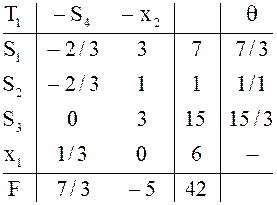
(проверьте на примере перехода от    правила  1) - 5) симплексного преобразования). Теперь  базисные,  свободные. Полученный ранее план     оказался опорным для таблицы   (почему?). Этот план можно снова «улучшить», так как в выражении  F  через свободные переменные  есть положительный коэффициент 5 (элемент (-5) в строке F); при   с ростом    первой обратится в нуль базисная переменная   (- наименьшее отношение в  столбце  ); к   применим симплексное преобразование с  разрешающим элементом на пересечении столбца   и строки   В результате получим таблицу   затем из нее аналогично таблицу 

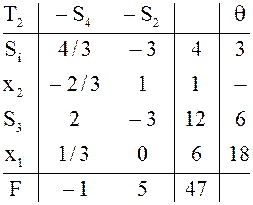
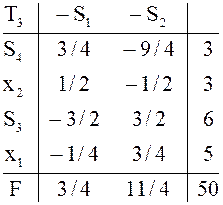
(Опорным планам   соответствуют вершины  ,  рис. 1). Таблица   не только допустима  (  тоже допустимы),  но и   удовлетворяет условию

строгой  оптимальности ( в строке F). По критерию оптимальности

  - единственный оптимальный план,   Таким образом, последовательное улучшение опорных планов привело к полному решению задачи ЛП; ответ, конечно, совпал с результатом графического решения. В заключение напомним, что в канонической модели задачи о ресурсах балансовые переменные – это остатки ресурсов. К «экономической» формулировке ответа в конце примера 6 можно добавить: при этом ресурсы   будут израсходованы полностью, а остатки ресурсов   равны шести  и трем  соответственно.

     Пример 8. Решить задачу ЛП    с ограничениями     

     Решение. Как и в предыдущем примере, приведем задачу к канонической форме и примем за базисные балансовые переменные. Такой записи задачи соответствует симплексная таблица    и опорный план   Улучшение плана    приводит к допустимой таблице   удовлетворяющей условию оптимальности,

     В строке F таблицы     есть нулевой  элемент; опорный план

,   оказывается не единственным оптимальным. Найдем все  оптимальные планы. Таблица   соответствует уравнениям        

Значения  F  не зависят от    и убывают с ростом   поэтому в оптимальных

планах необходимо, чтобы   а допустимые значения   находятся из неравенств      т. е. 

Таким образом,  все оптимальные планы имеют вид   ,    При    получаем опорный план   План   который получается при  так же будет  опорным (почему?). В графическом решении исходной задачи ЛП оптимальным планам   соответствует ребро четырехугольной области допустимых планов с вершинами в точках   (проверьте).

     Пример 9. Решить задачу ЛП   с ограничениями   .

     Решение. Здесь так же, как  и в двух предыдущих примерах, легко получаются «начальная» форма уравнений и соответствующая симплексная таблица:

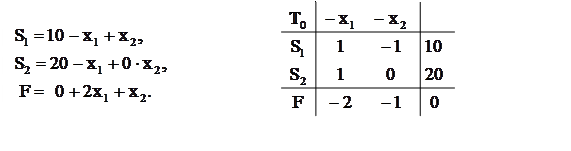
Обратим внимание на коэффициенты при свободной переменной    (столбец  ): коэффициент в выражении F положителен (в таблице  ), а среди коэффициентов при   в выражениях   нет отрицательных (в столбце    таблицы нет положительных элементов). Поэтому при   и неограниченном возрастании   значения   остаются неотрицательными, а значения F неограниченно возрастают, т. е. F не  ограничена на допустимых планах,  и задача ЛП не имеет оптимальных планов. Этот результат очевиден и при графическом решении исходной задачи (убедитесь в этом).

     В разобранных примерах (см. также упр. 11) хорошо видна тесная связь опорных планов с вершинами многоугольной области допустимых планов. Оказывает-ся,  что опорные планы в общем случае играют такую же роль, как вершины в задачах ЛП с наглядной геометрической интерпретацией. Это подтверждается следующими утверждениями, доказанными в теории ЛП.

     Теорема о допустимых опорных планах.  Если каноническая задача ЛП имеет допустимые планы, то среди них найдется опорный план.

     Теорема об оптимальных опорных планах. Если каноническая задача ЛП имеет оптимальные планы, то среди них найдется опорный план.