Линейное программирование. Некоторые примеры экономических задач, приводящих к модели линейного программирования. Геометрическая интерпретация и графическое решение задачи ЛП, страница 17

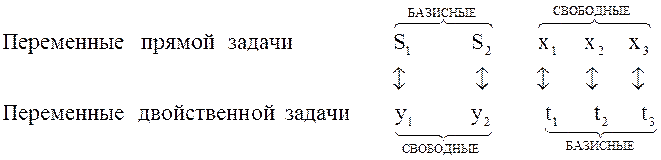
Запишем симплексные таблицы обеих задач, в которых  переменные   

приняты за базисные:

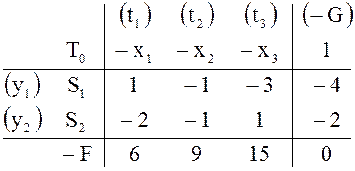
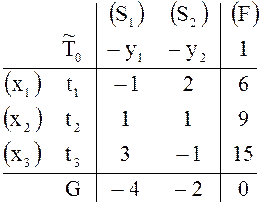
В таблицах   рядом с каждой  переменной записана в скобках соответствующая переменная двойственной задачи; добавлены также символы   в правых верхних углах. Благодаря этим дополнениям любое из равенств канонических форм обеих задач можно «прочитать» как в строке одной  из таблиц, так и в столбце другой (во втором случае надо использовать переменные, записанные в скобках). Например, первая строка   и первый столбец   являются записями эквивалентных равенств   и

 в последней строке    и последнем столбце   тоже записаны эквивалентные равенства    и   Связь таблиц   аналогична связи двух транспонированных относительно друг друга матриц: обозначения строк   в   переходят в обозначения  столбцов   числа  1,-1,-3,-4 первой строки    переходят в числа  -1, 1, 3, -4  первого столбца   и т.д.

     Таблица   допустима  (числа 6, 9, 5 неотрицательны), ее можно принять за начальную для решения двойственной задачи симплекс-методом. По инструкциям симплекс-метода находим разрешающий элемент 3 таблицы    В таблице   примем за разрешающий соответствующий элемент (-3) и выполним симплексные преобразования таблиц   В результате получим новые таблицы    

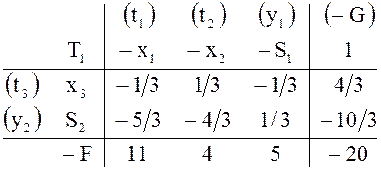
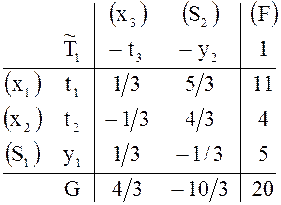
Таблицы   связаны между собой точно так же, как две предыдущие,   Каждая из них содержит системы уравнений, эквивалентные условиям прямой и двойственной задач. Продолжая решение двойственной задачи симплекс-методом, находим в  разрешающий элемент 4/3; в  принимаем за разрешающий соответствующий элемент (-4/3). После выполнения симплексных  преобразований получим таблицы 

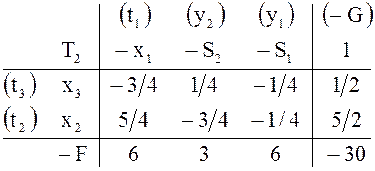
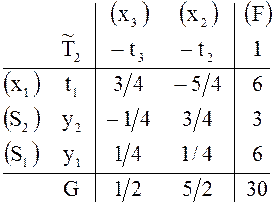
Допустимая таблица   удовлетворяет условию оптимальности (числа 1/2, 5/2 положительны).Ей соответствует единственный оптимальный опорный план двойственной задачи :  (свободные в ),  . Учитывая «транспонированность»  и соответствие  между переменными взаимодвойственных задач, по таблице   можно найти и  оптимальный опорный план () прямой задачи. Переменные   записанные в скобках в левом столбце   будут свободными в   следовательно   Переменные   записанные в скобках в верхней строке   будут базисными  в   следовательно   (см. строку  ). Очевидно, что    Аналогично оба оптимальных плана можно найти по таблице 

     Связь между симплексными таблицами прямой и двойственной задач, которая использовалась в примере 17, является основой нового способа решения задач ЛП, получившего название двойственного симплекс-метода.  В этом методе начальная и все следующие таблицы удовлетворяют  условию оптимальности вместо требования  допустимости в обычном симплекс-методе. Заключительная таблица дает оптимальный план или позволяет сделать вывод об отсутствии допустимых (и тем более оптимальных) планов.  Правила выбора разрешающего элемента в текущей симплексной таблице получаются  из соответствующих правил обычного симплекс-метода для двойственной задачи с учетом связей между таблицами двойственной пары.

Алгоритм двойственного симплекс метода

      Шаг 1. Объявить начальную симплексную таблицу (удовлетворяющую условию оптимальности) и соответствующий базисный план текущими.

       Шаг 2. Просмотреть столбец свободных членов текущей таблицы (кроме элемента в строке целевой функции).

       а) Если в столбце свободных членов нет отрицательных элементов (все ), то текущий базисный план – оптимальный.

       б) Если в столбце свободных членов  отрицательные элементы, выбирать среди них наибольший по модулю и объявить соответствующую строку разрешающей.

       Шаг 3. Просмотреть разрешающую строку текущей таблицы (кроме элемента в столбце свободных членов)

       а) Если в разрешающей строке нет отрицательных элементов (все ), то задача не имеет допустимых планов, и, следовательно, не разрешима.

       б) Если в разрешающей строке есть отрицательные элементы, для всех содержащих эти элементы столбцов вычислить и записать в строку    отношения коэффициентов строки целевой функции к соответствующим (отрицательным) элементам разрешающей строки – двойственные симплексные отношения.  Столбец с минимальным  по модулю  двойственным симплексным отношением объявить  разрешающим, элемент на пересечении разрешающего столбца с разрешающей строкой объявить разрешающим.