Линейное программирование. Некоторые примеры экономических задач, приводящих к модели линейного программирования. Геометрическая интерпретация и графическое решение задачи ЛП, страница 3

     После выполнения двух описанных выше преобразований задача ЛП общего вида сведется к задаче максимизации с требованием неотрицательности всех ее переменных; среди остальных ограничений задачи могут встречаться как равенства, так и неравенства. Чтобы свести такую задачу ЛП к стандартной форме,  надо исключить  все ограничения – равенства; для сведения к канонической форме – заменить систему ограничений – неравенств на эквивалентную систему ограничений, записанную в виде равенств и требований неотрицательности некоторых (дополнительно введенных) переменных.

     При исключении ограничений – равенств используются  известные методы линейной алгебры. Если все ограничения-равенства образуют несовместную систему линейных уравнений, то задача ЛП   не имеет допустимых и тем более оптимальных планов. Если эта система совместна и имеет ранг  r,  то с помощью метода Гаусса некоторые   переменных задачи можно выразить через остальные.  Подстановка этих выражений в целевую функцию и все ограничения-неравенства (включая и требования неотрицательности переменных) сводит задачу   к стандартной  форме; при этом число переменных уменьшается на  r.

      Для приведения задачи ЛП к  канонической форме вводятся дополнительные, так называемые балансовые, переменные; число таких переменных равно числу ограничений-неравенств (без учета требований неотрицательности переменных) исходной задачи.  Каждое ограничение – неравенство 

заменяется на эквивалентную ему пару ограничений 

 В случае неравенства со знаком   балансовая переменная   включается в  cоответствующее равенство со знаком минус.

     Рассмотрим примеры применения описанных выше преобразований формы задач ЛП.

  Пример 4. Привести к стандартной форме задачу ЛП

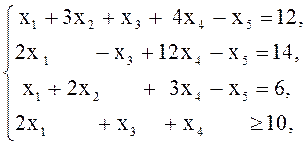
     Решение.   Решаем методом Гаусса систему ограничений-равенств

       ~       ~

 ~  .

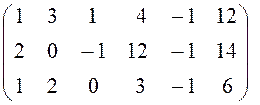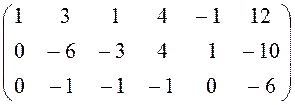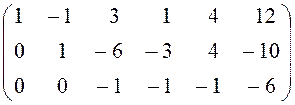Из полученной трапециевидной формы   системы последовательно выражаем  через   (обратный ход метода Гаусса):  

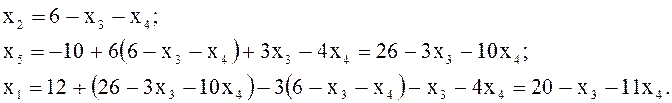
     Подставим полученные выражения в целевую функцию и ограничения-неравенства; одновременно заменим задачу минимизации  F  на максимизацию

После упрощений получим задачу ЛП

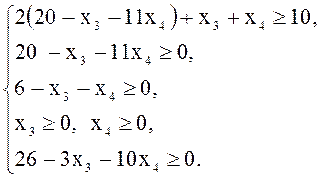
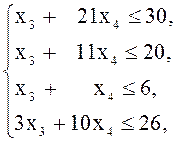
в стандартной форме, эквивалентную исходной. Если оптимальный план   и экстремальное значение целевой функции    задачи ЛП в стандартной форме уже найдены, то решением исходной  задачи будет план   и значение

     Пример 5. Привести к канонической форме задачу ЛП

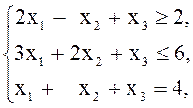
     Решение.  В данной модели нарушены следующие требования к канонической форме: направление оптимизации  минимизация (), а не максимизация  (); отсутствует требование неотрицательности переменной  кроме требований неотрицательности переменных  среди ограничений имеются еще два неравенства. Поэтому для сведения данной задачи ЛП к канонической форме надо последовательно произвести следующие три преобразования: заменить   на    везде, как в целевой функции, так и в ограничениях, заменить    и добавить к ограничениям требования    преобразовать два первых ограничения – неравенства в равенства с помощью балансовых переменных    ( вводится в первое неравенство со знаком минус,  - во второе со знаком плюс). В результате получим задачу линейного программирования в канонической форме

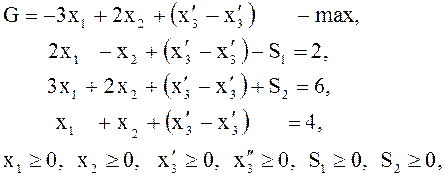
эквивалентную исходной.

     Если   и   оптимальный

план и значение задачи в канонической  форме, то 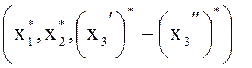    и    оптимальный план и значение исходной задачи.

     Модель  (4) - (6) задачи о ресурсах из примера 1 предыдущего параграфа представляет собой задачу  ЛП в стандартной форме. Фактически модель (4) - (6) просто совпадает с (14) - (16), только в первом случае использованы сокращенные записи для сумм  и из экономического смысла задачи о ресурсах в (4) - (6) предполагается, что   а в (14) – (16) числа   могут быть любого знака. Так как любую задачу  ЛП можно свести к стандартной форме (14) - (16), можно сказать, что любая задача ЛП эквивалентна задаче о ресурсах, если в последней допускаются отрицательные значения ее параметров