Линейное программирование. Некоторые примеры экономических задач, приводящих к модели линейного программирования. Геометрическая интерпретация и графическое решение задачи ЛП, страница 7

7. В  суточный рацион включаются два продукта питания   причем продукта   не более 200 единиц. Содержание витаминов А и В в единице каждого из продуктов,  минимальная  суточная   потребность в витаминах  и  стоимость

единицы каждого продукта заданы в таблице:

Определить рацион минимальной стоимости.

     8. Хозяйство имеет 600 га  пашни, трудовые ресурсы составляют 4000 чел.-дн. Урожайность зерновых и кормовых культур с 1 га  – 28 и 36 ц, затраты труда – 5 и 10 чел.-дн. на гектар. Определить наиболее эффективное сочетание зерновых и кормовых культур при условии, что  под кормовые культуры должно быть занято не менее 100 га  пашни, а доходы от 1 ц  зерновых и 1 ц кормовых культур совпадают.

     9. Используя замечание в конце данного параграфа, найти оптимальные планы и значения целевых функций  задач ЛП из упражнений 2б), 2в), 3а), 3в), 3г). Во всех случаях рассмотреть оба направления оптимизации.

     10. Найти    и соответствующие оптимальные планы задачи ЛП с ограничениями      если

          а)                                  б) 

          в)                                            г)  

Как изменится  решение, если удалить ограничение 

   11. Показать, что а) для любой вершины шестиугольника OABCDE (пример 6, рис.1) два ограничения-неравенства  выполнены как равенства; б) допустимый план    задачи (23)-(24) является вершиной области допустимых планов тогда и только тогда, когда для   некоторые два из неравенств (24) выполнены как равенства, причем коэффициенты при   в этих неравенствах образуют отличный от нуля определитель второго порядка. Сформулировать и обосновать утверждение, аналогичное б),  для стандартной задачи ЛП с тремя переменными.

4. Симплекс-метод

     Рассмотрим задачу ЛП в канонической форме (17)-(19). Без ограничения общности можно считать, что система (18) имеет бесконечное число решений, т. е. 

ранг системы  r  меньше числа переменных  n,  так как  в других случаях (каких?) задача ЛП решается тривиально (как?). Можно также считать, что все  m  уравнений независимы, т. е.  , так как при   лишние уравнения, являющиеся следствиями остальных, можно отбросить, не меняя множества решений системы. Поэтому везде далее будем считать, что   Для сокращения записей введем еще обозначение 

     При   по определению ранга, матрица системы содержит хотя бы один (возможно более одного) не равный нулю минор m-го порядка – базисный минор. Набор из  m  переменных называется  базисом, если соответствующие m  столбцов матрицы системы (18) образуют базисный минор. Если ясно, о каком  именно базисе идет речь, входящие в  него  m  переменных будем называть  базисными, а остальные   переменных – свободными. Из линейной алгебры известно, что систему (18) можно разрешить относительно базисных переменных. Если, например,  - базис, то (18) эквивалентна системе

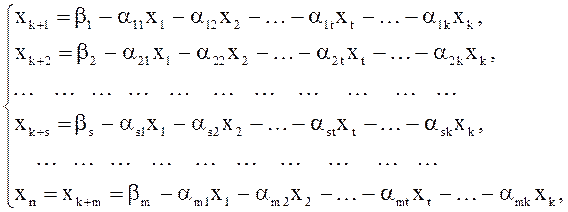                                      (25)

в которой базисные переменные выражены через свободные. Подставим выражение  (25) в (17):

После приведения подобных получим выражение целевой функции  через свободные переменные:

                                              .                                      (26)

     Систему всех уравнений (25), (26), эквивалентную  системе (17), (18), можно записать в виде  таблицы 2, которая называется симплексной таблицей задачи ЛП (17)-(19) в базисе   Из построения ясно, что симплексная таблица 2, как и любая симплексная таблица в другом базисе, представляет собой просто иную, более удобную запись  всех  условий  задачи  (17)-(19),   кроме   требований

неотрицательности переменных (19) (об этих требованиях надо всегда помнить).