Линейное программирование. Некоторые примеры экономических задач, приводящих к модели линейного программирования. Геометрическая интерпретация и графическое решение задачи ЛП, страница 22

     Решение. Ведению нового ресурса соответствует введение дополнительного ограничения   в стандартную модель задачи о ресурсах. Если оптимальный план исходной  задачи удовлетворяет дополнительному ограничению, то он, очевидно, остается оптимальным для задачи с этим дополнительным ограничением. В условии данного примера оптимальный план исходной задачи   не удовлетворяет дополнительному ограничению,   Чтобы найти новый оптимальный план, совсем не обязательно решать заново  задачу ЛП с дополнительным ограничением. Гораздо быстрее приводит к цели (и не только в данном примере) введение дополнительного ограничения в таблицу   исходной задачи.

     Новое ограничение   приведем к каноническому виду    (смысл переменной  - остаток нового ресурса). Чтобы ввести новое ограничение-равенство в  , отнесем   к базисным и заменим переменные    их выражениями через свободные переменные 

 таблицы  . Тогда новое равенство запишется в виде  

 или, после приведения подобных членов,

Введем в   строку, соответствующую этой форме записи нового ограничения. В результате получим таблицу   - одну из симплексных таблиц задачи с дополнительным ограничением:

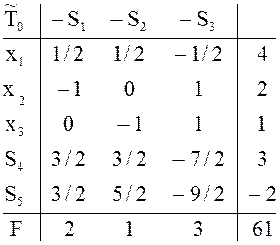
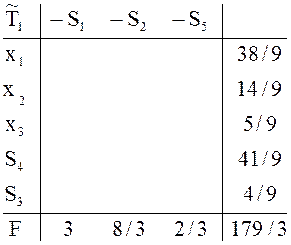
Таблица   удовлетворяет условию оптимальности (это следует из способа построения   ). Применяя двойственный симплекс-метод, уже после первого преобразования получим таблицу  , содержащую новый оптимальный  план    . Новый оптимальный план  хуже старого – доход от реализации всей произведенной продукции уменьшился  (). Этого и следовало ожидать, т. к. введение  дополнительного ограничения не может привести к увеличению максимального значения целевой функции (попробуйте  обосновать это утверждение и дать ему геометрическую интерпретацию).

     Пример 28. Технологические коэффициенты и доход от реализации единицы нового (четвертого) вида продукции равны 1, 3, 1, 2 и 10 соответственно. Выгодно ли введение в план производства нового вида продукции? Если да, найти новый оптимальный  план и величину максимального дохода.

     Решение. Обозначим объем производства нового вида продукции через    Стандартная модель задачи о ресурсах, учитывающая возможность производства нового  вида продукции, отличается от модели исходной  задачи дополнительными слагаемыми    в ограничениях и целевой функции:

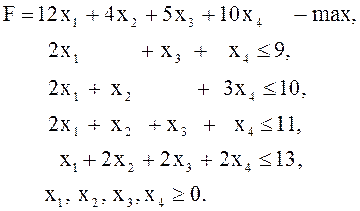
     Переменной   соответствует дополнительное ограничение 

 двойственной задачи о ценности ресурсов. Оптимальный план                                                    

 исходной задачи о ценности ресурсов не удовлетворяет этому ограничению,   Поэтому новое значение    минимума целевой функции   будет больше , чем старое значение  (сравните с неравенством  в конце предыдущего примера). Из первой теоремы  двойственности следует, что   Здесь  -новое значение максимального дохода от реализации всей произведенной  продукции; неравенство   означает, что в условиях данного примера введение в план производства нового вида продукции выгодно.

     Чтобы найти новый оптимальный план    и  , введем в таблицу   дополнительный столбец, соответствующей переменной    прямой задачи и переменной   из канонической формы  

 нового ограничения двойственной задачи. Элементы дополнительного столбца находятся так же, как элементы дополнительной строки в  предыдущем примере, вместо нового ограничения прямой задачи надо использовать новое ограничение двойственной задачи. Базисные переменные двойственной задачи

 выражаются через свободные переменные   по формулам (см. столбцы таблицы  ):

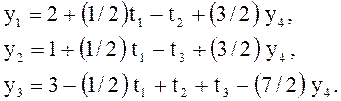
После подстановки этих выражений в равенство     новое  ограничение запишется в виде

Результатом введения в  дополнительного столбца, соответствующего последнему равенству, будет симплексная таблица   новой задачи: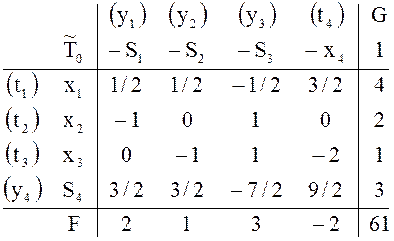    

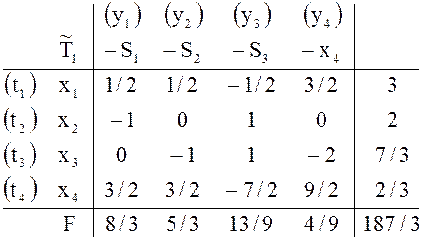
Таблица     допустима (это следует из способа ее построения). Применяя обычный симплекс метод, уже после первого преобразования получим таблицу    содержащую новый оптимальный план:

     Введение в план производства нового вида продукции привело к увеличению дохода на