Линейное программирование. Некоторые примеры экономических задач, приводящих к модели линейного программирования. Геометрическая интерпретация и графическое решение задачи ЛП, страница 20

     С помощью симплекс-метода, обычного или двойственного, можно не только находить оптимальные планы задач двойственной пары, но и исследовать, как меняются эти планы при различных изменениях в ограничениях и целевых функциях рассматриваемых задач.

      Покажем, как проводятся такие исследования на примере конкретной  пары «задача о ресурсах – задача о ценности ресурсов» (см. примеры 11, 15, 20):

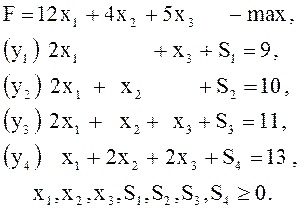
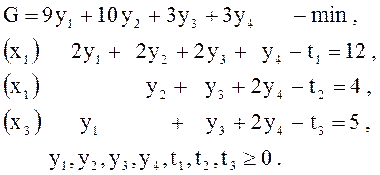
     Для удобства изложения запишем начальную и заключительную таблицы цепочки, полученной при решении  симплекс-методом первой из этих задач, задачи о ресурсах (см.  в примере 11 и   в примере 20):

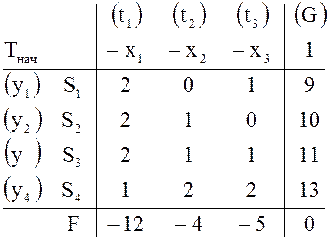
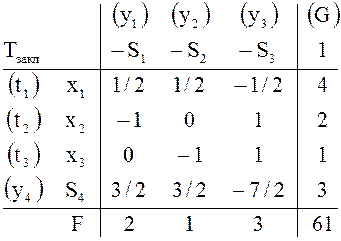
     Пример 21 (Изменение правых частей ограничений). В исходной задаче о ресурсах изменились только запасы ресурсов (правые части ограничений), новые значения запасов равны    

 соответственно. Записать симплексную таблицу новой задачи в базисе таблицы   сформулировать правила построения такой таблицы. Показать, что при  достаточно малых значениях приращений   ценности ресурсов не изменяются.

     Решение. Введем обозначения  

  Тогда условия задачи с измененными  запасами запишутся в виде

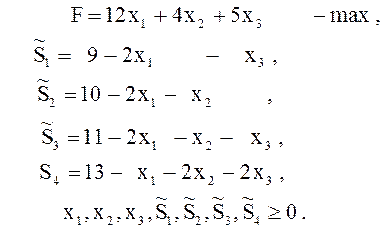
Эта запись отличается от записи уравнений в таблице   только заменой 

  на     cоответственно. Так как системы уравнений в таблицах

 эквивалентны, уравнение новой задачи можно привести к виду

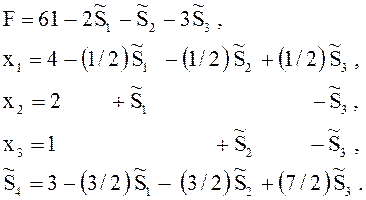
     После замены     на их выражения    получим систему, соответствующую искомой таблице   ,

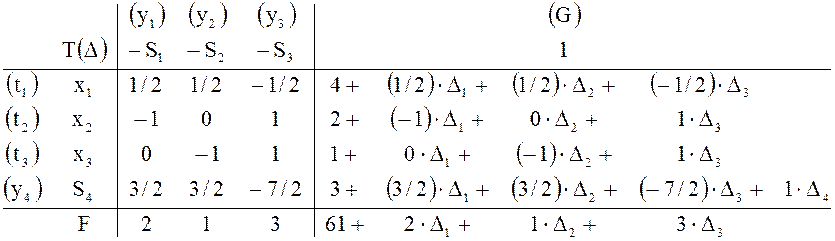
     Правила построения таблицы    

     Таблица    отличается от   только значениями элементов столбца свободных членов. К свободным членам таблицы    надо  прибавить поправки, зависящие линейно от приращений   Приращения    связаны с переменными   которые были базисными в  и стали свободными в

; эти приращения входят в поправки с коэффициентами, равными элементам

соответствующей строки таблицы   из столбцов   Приращение    

связано с переменной    которая осталась базисной в  ;  входит только в поправку свободного члена строки     причем с коэффициентом, равным единице.

     При достаточно малых приращениях     таблица   удовлетворяет (строго) критерию оптимальности – в ней положительны как элементы столбца свободных членов   (они близки к положительным значениям 4, 2, 1, 3  из   ), так и элементы строки F (совпадают с значениями 2, 1, 3  из   ). Совпадение ценностей ресурсов в исходной задаче и задаче с малыми изменениями запасов ресурсов следует из совпадения строк F (без свободных членов) в таблицах     и

; в каждой их этих задач 

      Пример 22  (Изменение коэффициентов целевой функции). В исходной  задаче о ресурсах изменились только доходы от реализации единицы готовой продукции (коэффициенты целевой функции), новые значения доходов равны    соответственно.

Записать симплексную таблицу новой задачи в базисе таблицы   Показать, что при достаточно малых значениях приращений доходов  оптимальный план задачи не изменится.

     Решение. Изменению коэффициентов целевой функции в задаче о ресурсах соответствует изменение правых частей ограничений в двойственной задаче (о ценности ресурсов). Повторим все рассуждения предыдущего примера, заменяя в них уравнения задачи о ресурсах на уравнения двойственной задачи. В результате получим, что искомая таблица   задачи о ресурсах с измененными доходами отличается от таблицы  только  значениями  элементов строки F и имеет вид

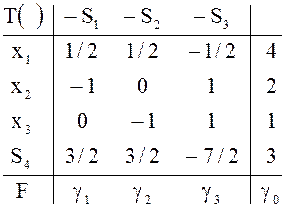
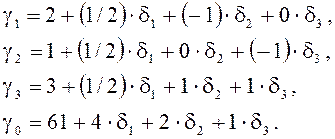
К элементам  строки  F  таблицы   прибавляются поправки, зависящие линейно от приращений  . Коэффициенты при   в этих поправках равны элементам соответствующего столбца таблицы    из строк    (сформулируйте самостоятельно правила вычисления поправок в ситуации, когда некоторые  из свободных переменных    таблицы    остаются свободными и в таблице). 

      При достаточно малых приращениях  элементы   строки F положительны  и таблица   удовлетворяет критерию оптимальности. В этом случае оптимальный план   задачи с измененными доходами совпадает с оптимальным планом исходной задачи о ресурсах.

     Пример 23. В исходной задаче о ресурсах запасы 9, 10, 11, 13  изменились и составляют  9, 10, 14, 8 соответственно. Найти новый оптимальный план  производства.