Линейное программирование. Некоторые примеры экономических задач, приводящих к модели линейного программирования. Геометрическая интерпретация и графическое решение задачи ЛП, страница 19

В примере 21 следующего п.7 будет показано, что    остается  единственным оптимальным планом задачи, двойственной к задаче о ресурсах с  измененными  запасами     если приращения запасов   достаточно малы. Максимальным значением дохода будет величина

Из последнего равенства видно, что при   малые изменения запаса i-го ресурса не меняют величину максимального дохода   такие ресурсы называются недефицитными. Ресурсы, для которых  , называются  дефицитными - увеличение (уменьшение) из запасов увеличивает (уменьшает) доход   Числа   определяют скорость возрастания   при  увеличении соответствующего запаса и называются ценностями  или теневыми ценами ресурсов в данных условиях производства; задача, двойственная к задаче о ресурсах, называется задачей о ценности ресурсов.

     Используя понятие дефицитности и теневых цен ресурсов, можно дать экономическое истолкование постановке двойственной задачи (31) – (33) и утверждениям теорем двойственности. В частности, вторая группа уравнений теоремы 2 означает, что дефицитные ресурсы   в оптимальных планах производства расходуются полностью  , а все ресурсы, которые расходуются не полностью  , являются  недефицитными  .

       Пример 20. Построить модель задачи о ценности ресурсов для задачи о ресурсах  из примера 11. Найти ценности  и определить статус (дефицитные, недефицитные) ресурсов, указать самый ценный ресурс.

        Решение. Моделью задачи о ценности ресурсов является задача ЛП, двойственная к модели самой задачи о ресурсах. Условие этой задачи записано в примере15. Ценности ресурсов, т. е.  компоненты   оптимального плана двой-

ственной  задачи, можно найти непосредственно по заключительной таблице   прямой задачи (см. пример 11) аналогично тому, как это сделано в примере 17. Записанные в скобках переменные   двойственной задачи

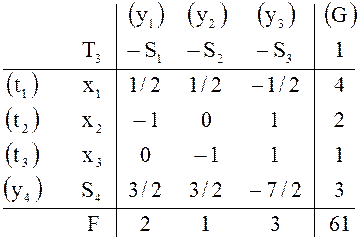
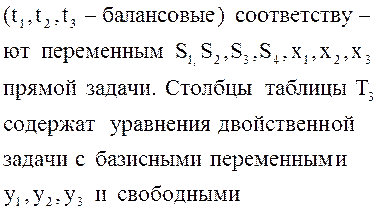
В соответствующем базисном плане    

  Из оптимальности    для  прямой задачи  следует, что   

оптимальный план двойственной задачи. Таким образом, четвертый ресурс недефицитный  , все остальные – дефицитные. Самым ценным является третий ресурс   

Упражнения

      18. Решить задачу ЛП, используя графический метод решения задачи, двойственной к исходной:

а)     б)

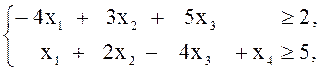
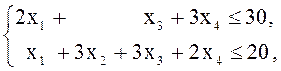
      19. Построить двойственную задачу, решить одну  из них и записать оптимальный план и записать оптимальный план другой задачи:

а)                    б)  

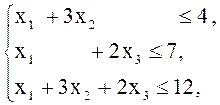
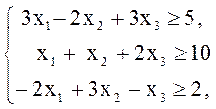
      20. Решить двойственным симплекс-методом

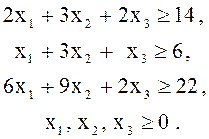
       21. Минимальное количество автобусов, обеспечивающих потребность в пассажирских перевозках на городских маршрутах, остается постоянным в пределах каждого из шести четырехчасовых интервалов  0 часов – 4 часа, 4 часа – 8 часов, …,

20часов – 24 часа, и составляет 4, 8, 10, 7, 12, 4 автобуса соответственно.  Каждый автобус используется непрерывно в течении восьми часов один раз в сутки, начало смены совпадает с началом  одного из указанных четырехчасовых интервалов времени. Требуется определить минимальное значение общего количества автобусов, выходящих на городские маршруты в течение суток. Сколько автобусов занято при этом в каждой из  шести восьмичасовых смен?

     22. На складе предприятия имеются заготовки (бруски) длиной 8,1 м. Из этих заготовок требуется изготовить 100 комплектов более коротких заготовок, в один комплект входят два бруска длиной 3 м. и по одному бруску длиной 2м. и 1,5м. Необходимо раскроить исходный материал так, чтобы получить требуемое количество комплектов коротких заготовок с минимальными отходами.  У к а з а н и е :

Рассмотреть все способы раскроя заготовок длины 8,1 м., в которых отходами будут бруски длиной менее, чем 1,5 м. Всего таких способов будет 10. Один из них, например, дает 2 заготовки длиной 3м. и одну заготовку длиной 2м.; при этом в отходы пойдет брусок длиной       

7. Исследование зависимости оптимальных планов от исходных данных

задачи ЛП