![]()
![]() (28)
(28)
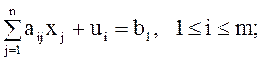 (29)
(29)
![]() (30)
(30)
В
задаче (28) – (30) выбор начальной симплексной таблицы очевиден из самой формы
уравнений (29) - за базисные надо принять искусственные переменные ![]() предположение
предположение ![]() обеспечивает
допустимость этой таблицы. В результате применения симплекс-метода к невырожденной
вспомогательной задаче (ограничимся только таким случаем) через конечное
число шагов будет найдена заключительная симплексная таблица
обеспечивает
допустимость этой таблицы. В результате применения симплекс-метода к невырожденной
вспомогательной задаче (ограничимся только таким случаем) через конечное
число шагов будет найдена заключительная симплексная таблица ![]() В задаче (28) – (30) целевая функция
В задаче (28) – (30) целевая функция ![]() ограничена сверху:
ограничена сверху: ![]() в
силу требований
в
силу требований ![]() из (30). Поэтому выполнение
условий шага 3а) невозможно, таблица
из (30). Поэтому выполнение
условий шага 3а) невозможно, таблица ![]() удовлетворяет
условиям шага 2а) и ей соответствует оптимальный опорный план
удовлетворяет
условиям шага 2а) и ей соответствует оптимальный опорный план ![]()
![]()
Исследуем связь исходной задачи (17) – (19) и вспомогательной
(28) – (30). Пусть исходная задача имеет допустимые планы и ![]()
![]() один из них. Тогда
план
один из них. Тогда
план ![]() (с теми же, что и в Х, значениями переменных
исходной задачи и нулевыми значениями искусственных переменных) будет
допустимым для вспомогательной задачи, т. к. при
(с теми же, что и в Х, значениями переменных
исходной задачи и нулевыми значениями искусственных переменных) будет
допустимым для вспомогательной задачи, т. к. при ![]() ограничения
вспомогательной задачи совпадают с ограничениями исходной. При этом
ограничения
вспомогательной задачи совпадают с ограничениями исходной. При этом ![]() Учитывая, что
Учитывая, что ![]() на всех
допустимых планах, заключаем, что
на всех
допустимых планах, заключаем, что ![]() - оптимальный и
- оптимальный и ![]() Итак, в случаях, когда исходная задача имеет
допустимые планы, во вспомогательной задаче обязательно получится
Итак, в случаях, когда исходная задача имеет
допустимые планы, во вспомогательной задаче обязательно получится ![]() Последнее утверждение можно сформулировать
таким образом.
Последнее утверждение можно сформулировать
таким образом.
Если во вспомогательной задаче ![]() то в исходной задаче
нет допустимых планов и она не имеет решения.
то в исходной задаче
нет допустимых планов и она не имеет решения.
Осталось выяснить, что дает для исходной задачи результат ![]() во вспомогательной. Так как
во вспомогательной. Так как ![]() неотрицательны, равенство
неотрицательны, равенство![]()
![]() возможно только при
возможно только при ![]() Но тогда в
силу невырожденности вспомогательной задачи ни одна из искусственных
переменных не может оказаться базисной в заключительной таблице
Но тогда в
силу невырожденности вспомогательной задачи ни одна из искусственных
переменных не может оказаться базисной в заключительной таблице ![]() т. е. все они свободные (записаны в
верхней строке таблицы
т. е. все они свободные (записаны в
верхней строке таблицы ![]() ). Таблица
). Таблица ![]() (без строки H) – одна из
форм записи системы (29). При
(без строки H) – одна из
форм записи системы (29). При ![]()
![]() система
(29) превращается в систему (18). Легко понять, что, вычеркивая из
система
(29) превращается в систему (18). Легко понять, что, вычеркивая из ![]() строку Н и столбцы
строку Н и столбцы ![]() , получим одну из записей системы (18), т.
е. симплексную таблицу
, получим одну из записей системы (18), т.
е. симплексную таблицу ![]() исходной задачи (17) –
(19) (без строки F). Таблица
исходной задачи (17) –
(19) (без строки F). Таблица ![]() допустима, так как
столбец свободных членов остался
допустима, так как
столбец свободных членов остался
тем
же, что и в допустимой таблице ![]() Строку F можно
найти, подставляя в вы-
Строку F можно
найти, подставляя в вы-
ражение
(17) целевой функции исходной задачи вместо базисных переменных таблицы ![]() их выражения через свободные (эти
выражения содержатсяв самой
их выражения через свободные (эти
выражения содержатсяв самой ![]() .
Таким образом, приходим к следующему выводу.
.
Таким образом, приходим к следующему выводу.
Если во вcпомогательной задаче ![]() то ее
заключительная симплексная таблица
то ее
заключительная симплексная таблица ![]() легко перестраивается в
начальную допустимую симплексную таблицу исходной задачи.
легко перестраивается в
начальную допустимую симплексную таблицу исходной задачи.
Замечание. При вырожденности
вспомогательной задачи возможна ситуация, когда ![]() но не
все искусственные переменные оказались свободными в заключительной таблице
но не
все искусственные переменные оказались свободными в заключительной таблице ![]() В таких случаях всегда существует последовательность
симплексных преобразований (не изменяющих опорный план), после выполнения
которых все искусственные переменные становятся свободными. В данных указаниях
примеры с вырожденными вспомогательными задачами не рассматриваются.
В таких случаях всегда существует последовательность
симплексных преобразований (не изменяющих опорный план), после выполнения
которых все искусственные переменные становятся свободными. В данных указаниях
примеры с вырожденными вспомогательными задачами не рассматриваются.
Разберем несколько примеров решения задач ЛП с использованием описанного выше метода нахождения начальной допустимой симплексной таблицы.
Пример 12. Решить задачу ЛП ![]() с ограничениями
с ограничениями
![]()
![]() ,
, ![]()
![]()
Решение. Приведем задачу к канонической форме
![]()
![]()
![]()
![]()
![]()
![]()
Воспользуемся
тем, что в первом и втором уравнении есть «очевидные» базисные переменные ![]() каждая из них входят только в одно
уравнение, причем с положительным коэффициентом. Введем всего одну
искусственную переменную u в третье уравнение. Вспомогательная задача имеет
следующий вид (требования неотрицательности опущены):
каждая из них входят только в одно
уравнение, причем с положительным коэффициентом. Введем всего одну
искусственную переменную u в третье уравнение. Вспомогательная задача имеет
следующий вид (требования неотрицательности опущены):
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.