Линейное программирование. Некоторые примеры экономических задач, приводящих к модели линейного программирования. Геометрическая интерпретация и графическое решение задачи ЛП, страница 13

    Смысл переменных - остатки  ресурсов. В стандартной форме - три переменные, графическое решение практически невозможно (попробуйте). Решим задачу симплекс-методом. Начальная таблица  здесь  (как и в любой задаче о ресурсах) находится просто: за базисные надо выбрать переменные  . Далее цепочка таблиц определяется шагами симплекс-метода однозначно.

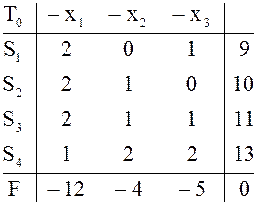
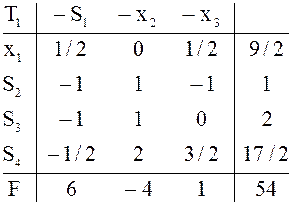
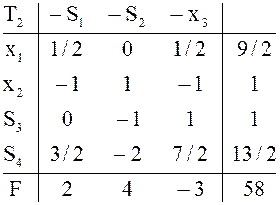
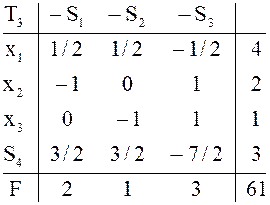
     Таблица   допустима и удовлетворяет условию строгой оптимальности. По критерию оптимальности  - единственный  оптимальный план и  . В экономических терминах это означает, что максимальный доход равен 61 и достигается только одним способом – объемы производства трех видов продукции должны быть равны 4, 2 и 1(в соответствующих единицах). При этом ресурсы первых трех видов будут израсходованы полностью, а остаток  четвертого ресурса   составит три единицы.

Упражнения

12. В хозяйстве имеются 850 га пашни, 15000 т органических удобрений, трудовые ресурсы составляют 50 000 чел.-дн. Хозяйство специализируется на производстве трех культур: капусте, картофеле и многолетниx травax на сено. Затраты труда (чел.-дн.), расход удобрений (т) и выход валовой продукции в денежном выражении (руб.) в расчете на 1 га составляют: для капусты – 50, 20, 1000; для картофеля – 30, 15, 800; для трав – 10, 10, 200. Найти оптимальное сочетание  посевов трех культур.

     13. Цех выпускает три вида изделий, располагая при этом сырьем четырех видов А, Б, В, Г в количествах 18, 16, 8, 6 ед. соответственно. Нормы затрат каждого вида сырья на одно изделие  первого вида составляют соответственно 1, 2, 1 , 0; второго вида 2, 1, 1, 1 и третьего вида 1, 1, 0, 1. Прибыль от  реализации одного изделия первого вида  равна 3 руб., второго – 4 руб., третьего – 2 руб. Составить план производства  трех видов изделий, максимизирующий прибыль.

     14. Механический завод при изготовлении двух типов деталей использует токарное, фрезерное и сварочное  оборудование. Обработку каждой детали можно вести двумя различными технологическими способами. Полезный фонд времени работы каждой  группы оборудования (в станко-часах), нормы расхода времени при обработке детали на соответствующем оборудовании по данному технологическому способу и прибыль от выпуска единицы детали каждого вида по каждому из способов приведены в таблице: 

Составить оптимальный план загрузки оборудования, обеспечивающий заводу максимальную прибыль.

     15. Привести (если требуется) к каноническому виду, найти начальную симплексную таблицу и решить симплекс-методом следующие задачи ЛП:

     а)  с ограничениями

     б) с ограничениями

в) с ограничениями

     г) с ограничениями 

          .

     16. Решить графически задачу из примера 10. Какие особенности ограничений-неравенств обуславливают вырожденность этой задачи?

5. Нахождение начальной симплексной таблицы

     Допустимая симплексная таблица, с которой начинаются вычисления симплекс-метода, не  всегда находится так просто, как  в  примерах 7-11. В задаче   о диете  (7) - (9), например, после ее приведения к канонической форме, ограничения – равенства имеют вид    Очевидный выбор переменных    в качестве базисных (тогда - свободные) приводит к недопустимой таблице: при   значения   базисных переменных отрицательны. Изложим  один из методов нахождения начальной  симплексной таблицы в общем случае.

     Пусть требуется найти начальную  симплексную таблицу задачи ЛП в канонической форме (17) – (19). Без ограничения общности будем предполагать, что все правые части уравнений (18) неотрицательны,    если  достаточно умножить соответствующее уравнение на (-1). Введем в левые части уравнений (18) искусственные переменные   и рассмотрим  вспомогательную  каноническую задачу ЛП: