Решение. Симплексная таблица ![]() задачи с
измененными запасами, построенная с помощью заключительной таблицы
задачи с
измененными запасами, построенная с помощью заключительной таблицы ![]() исходной задачи о ресурсах, удовлетворяет условию
оптимальности при любых значениях приращений
исходной задачи о ресурсах, удовлетворяет условию
оптимальности при любых значениях приращений
![]() (см. пример 21). Поэтому
(см. пример 21). Поэтому ![]() всегда можно использовать как
начальную для решения задачи с измененными запасами двойственным симплекс-методом.
В условиях данного примера имеем:
всегда можно использовать как
начальную для решения задачи с измененными запасами двойственным симплекс-методом.
В условиях данного примера имеем: ![]()
![]() Далее находим свободные члены таблицы
Далее находим свободные члены таблицы ![]() :
:
![]()
![]()
![]()
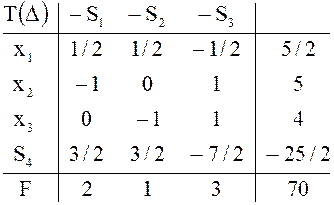
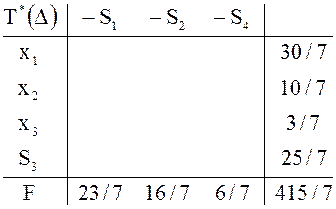
Таблица ![]() , содержащая оптимальный план
, содержащая оптимальный план ![]()
![]()
![]()
![]() новой задачи, получается с помощью двойственного
симплекс-метода уже после первого симплексного преобразования. Для
нахождения нового оптимального плана симплекс-методом без использования
заключительной таблицы исходной задачи пришлось бы выполнить не менее трех
симплексных преобразований (почему?).
новой задачи, получается с помощью двойственного
симплекс-метода уже после первого симплексного преобразования. Для
нахождения нового оптимального плана симплекс-методом без использования
заключительной таблицы исходной задачи пришлось бы выполнить не менее трех
симплексных преобразований (почему?).
Пример 24. В исходной задаче о ресурсах доходы 12, 4, 5 от реализации трех видов продукции изменились и составляют 12, 2, 7 соответственно. Найти новый оптимальный план производства.
Решение. Симплексная таблица ![]() задачи
с измененными доходами, построенная с помощью таблицы
задачи
с измененными доходами, построенная с помощью таблицы ![]() исходной
задачи, допустима при любых значениях приращений
исходной
задачи, допустима при любых значениях приращений ![]() (см. пример 22). Поэтому
(см. пример 22). Поэтому ![]() всегда можно использовать как
начальную для решения задачи с измененными доходами сим-
всегда можно использовать как
начальную для решения задачи с измененными доходами сим-
плекс-методом.
В условиях данного примера ![]()
![]()
![]() Далее
находим элементы строки F таблицы
Далее
находим элементы строки F таблицы ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
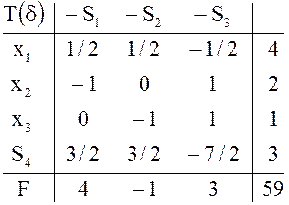
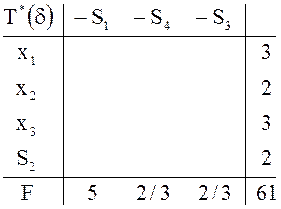
Как
и в предыдущем примере, использование заключительной таблицы исходной задачи
позволяет найти новый оптимальный план быстрее, чем при «прямом» решении
задачи с измененными условиями симплекс-методом. Таблица ![]() , содержащая новый оптимальный план
, содержащая новый оптимальный план ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() получается уже после первого
преобразования таблицы
получается уже после первого
преобразования таблицы ![]() . В отличии от
предыдущего примера разрешающий элемент выбирается по правилам обычного (а не
двойственного) симплекс-метода.
. В отличии от
предыдущего примера разрешающий элемент выбирается по правилам обычного (а не
двойственного) симплекс-метода.
Пример 25. В условии изменилась только величина запаса самого ценного ресурса. При каких изменениях этой величины ценности ресурсов не меняются?
Решение. Ценности ресурсов ![]() найдены в примере 20,
самым ценным оказался третий ресурс. Рассмотрим таблицу
найдены в примере 20,
самым ценным оказался третий ресурс. Рассмотрим таблицу ![]() которая получается из таблицы
которая получается из таблицы ![]() примера 21 при
примера 21 при ![]()
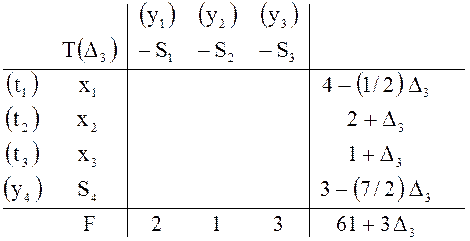
![]() - одна из симплексных таблиц задачи, в
которой по сравнению с исходной изменилась (получила приращение
- одна из симплексных таблиц задачи, в
которой по сравнению с исходной изменилась (получила приращение ![]() ) только величина запаса третьего ресурса.
Таблице
) только величина запаса третьего ресурса.
Таблице ![]() соответствует опорный план
соответствует опорный план ![]() задачи о ценности ресурсов,
компоненты которого совпадают с ценностями ресурсов исходной задачи. Этот
опорный план будет оптимальным при тех значениях
задачи о ценности ресурсов,
компоненты которого совпадают с ценностями ресурсов исходной задачи. Этот
опорный план будет оптимальным при тех значениях ![]() , для
которых
, для
которых ![]() допустима, т. е. при выполнении системы
неравенств
допустима, т. е. при выполнении системы
неравенств ![]()
![]() Решая эту систему,
получим
Решая эту систему,
получим ![]()
Таким образом ценности ресурсов не меняются, если запас самого ценного (третьего) ресурса изменяется в пределах от 11-1=10 до 11+(6/7).
Пример 26. В условии изменилась только величина максимального из доходов от реализации единицы продукции. При каких изменениях этой величины оптимальный план производства не меняется?
Решение. Максимальный из доходов от реализации единицы продукции в
исходной задаче имеет продукция первого вида. Предположим, что величина этого
дохода изменилась и ее новое значение равно ![]() Одной
из симплексных таблиц новой задачи будет таблица
Одной
из симплексных таблиц новой задачи будет таблица ![]() в
которую превращается
в
которую превращается ![]() (см. пример 22) при
(см. пример 22) при ![]()
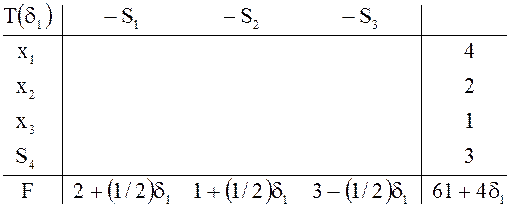
Таблице
![]() соответствует опорный план
соответствует опорный план ![]()
![]()
![]() , совпадающий с оптимальным планом исходной задачи о
ресурсах. Этот опорный план будут оптимальным при тех значениях
, совпадающий с оптимальным планом исходной задачи о
ресурсах. Этот опорный план будут оптимальным при тех значениях ![]() , для которых
, для которых ![]() удовлетворяет
условию оптимальности, т. е. при выполнении системы неравенств
удовлетворяет
условию оптимальности, т. е. при выполнении системы неравенств ![]() Решая эту систему, получим
Решая эту систему, получим ![]() Таким образом оптимальный план производства
не меняется, если доход от реализации первого вида продукции изменяется в
пределах от 12 – 2=10 до 12+6=18.
Таким образом оптимальный план производства
не меняется, если доход от реализации первого вида продукции изменяется в
пределах от 12 – 2=10 до 12+6=18.
Пример 27. Для улучшения качества продукции в процесс производства вводится новый (пятый) вид ресурса. Технологические коэффициенты и запас нового ресурса равны 1, 2, 3 и 9 соответственно. Найти оптимальный план производства и величину максимального дохода в новых условиях.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.