![]()
![]() .
.
В начальной таблице ![]() с базисными переменными
с базисными переменными ![]() , u целевую функцию Н надо выразить через свободные
переменные
, u целевую функцию Н надо выразить через свободные
переменные ![]()
![]()
![]() Решение вспомогательной задачи заканчивается
на таблице
Решение вспомогательной задачи заканчивается
на таблице ![]()
![]()
![]()
![]()
![]()
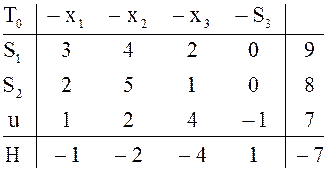
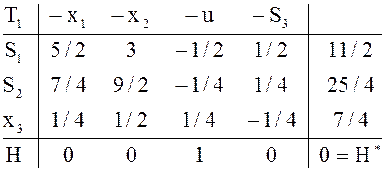
Здесь ![]() перестраиваем в начальную таблицу
перестраиваем в начальную таблицу ![]() для исходной зада-
для исходной зада-
чи
– вычеркиваем строку Н и столбец u и находим выражение F через свободные переменные ![]()
![]()
![]()
Затем
записываем ![]() следующая таблица
следующая таблица ![]() уже
удовлетворяет условию оптимальности .
уже
удовлетворяет условию оптимальности .
![]()
![]()
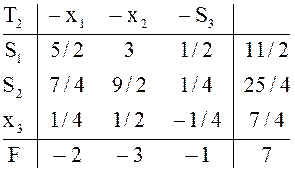
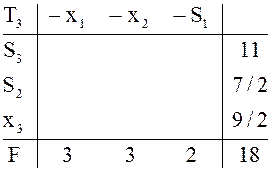
Обратите внимание на «неправильный» выбор разрешающего столбца в ![]() , что было бы при «правильном»? В
, что было бы при «правильном»? В ![]() как и в примере
10, внутренние элементы
как и в примере
10, внутренние элементы
не вычисляются.
Ответ: ![]()
![]() .
.
Пример 13. Решить задачу ЛП
![]()
![]()
![]()
![]()
Решение. Исходная задача уже
дана в канонической форме. Вводим искусственные переменные ![]() в оба уравнения, для вспомогательной
задачи сразу записываем начальную симплексную таблицу
в оба уравнения, для вспомогательной
задачи сразу записываем начальную симплексную таблицу ![]() Обратите
внимание на строку Н.
Обратите
внимание на строку Н.
|
![]()
![]()
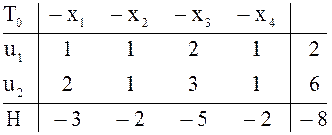
![]()
![]()
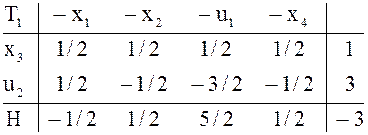
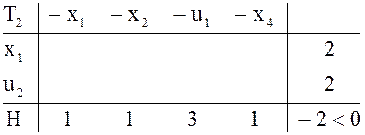
В
![]() решение вспомогательной задачи
закончено,
решение вспомогательной задачи
закончено, ![]()
![]()
Ответ: в задаче нет допустимых планов, она не имеет решения.
Заметим,
что противоречивость ограничений можно обнаружить, вычитая из удвоенного 1-го
уравнения![]() 2-е.
Получим
2-е.
Получим ![]() что противоречит
что противоречит ![]()
![]()
Пример 14. Решить задачу ЛП
![]()
![]()
![]()
![]()
![]()
Решение. Задача имеет
каноническую форму , ![]() можно использовать как начальную
базисную, искусственные переменные
можно использовать как начальную
базисную, искусственные переменные ![]() вводим только во второе
и третье уравнения.
вводим только во второе
и третье уравнения.
![]()
![]()
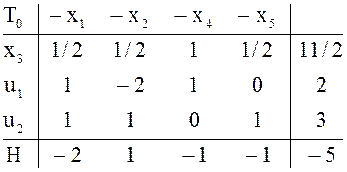
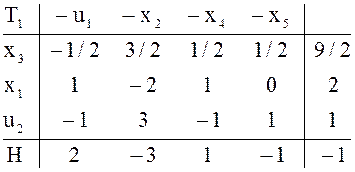
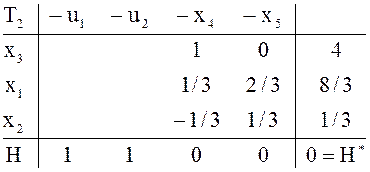
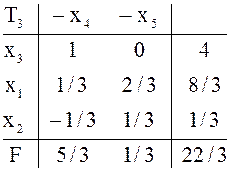
Решение
вспомогательной задачи заканчивается в ![]() перестраивается
в начальную
перестраивается
в начальную ![]() для исходной задачи. Функцию F
выражаем через свободные переменные
для исходной задачи. Функцию F
выражаем через свободные переменные![]() таблицы
таблицы ![]()
![]()
![]()
![]()
Начальная таблица ![]() уже удовлетворяет условию
оптимальности.
уже удовлетворяет условию
оптимальности.
Ответ: ![]()
Упражнения
17. Найти с помощью вспомогательной задачи начальную симплексную таблицу и решить симплекс–методом следующие задачи ЛП:
а) ![]() с
ограничениями
с
ограничениями ![]()
![]()
![]()
![]()
![]()
б) ![]() с
ограничениями
с
ограничениями ![]()
![]()
![]()
![]()
в) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
6. Двойственность в линейном программировании
Понятие двойственности является одним из важнейших в теории ЛП. С каждой задачей ЛП связывается другая вполне определенная задача, которая называется двойственной к исходной (прямой) задаче. Изучение связей между прямой и двойственной задачами помогает понять свойства каждой из них. Понятие двойственности и связанный с ним двойственный симплекс-метод решения задач ЛП используются при анализе зависимости оптимальных планов от изменений в условиях задачи ЛП.
Двойственной к стандартной задаче (14) – (16) называется задача ЛП от m переменных ![]() вида
вида
![]() (31)
(31)
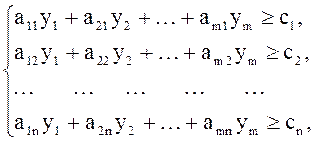 (32)
(32)
![]() (33)
(33)
Связь между условиями прямой задачи (14) – (16) и двойственной (31) – (33) показана схематически в таблице 5:
Таблица 5
![]()
![]()
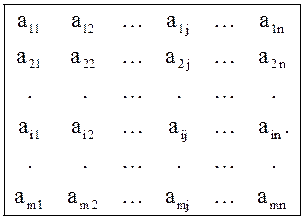
![]()
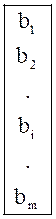
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.