Пусть ![]() - планируемый объем
перевозок из
- планируемый объем
перевозок из ![]() Тогда план перевозок задается
набором (матрицей) из
Тогда план перевозок задается
набором (матрицей) из ![]() чисел
чисел ![]() и модель транспортной задачи имеет вид
и модель транспортной задачи имеет вид
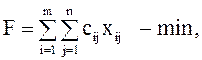 (10)
(10)
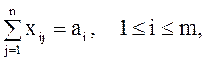 (11)
(11)
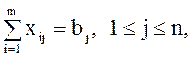 (12)
(12)
![]() (13)
(13)
Другие важные примеры
экономических задач, приводящих к аналогичным математическим моделям, можно
найти, например, в книгах ![]()
![]() 2.
Постановка задачи ЛП. Различные формы задач ЛП
2.
Постановка задачи ЛП. Различные формы задач ЛП
и их эквивалентность
Математические модели различных по содержательному смыслу экономических задач, рассмотренных выше, имеют много общего. Во всех примерах соответствующая математическая задача может быть сформулирована следующим образом: Максимизировать или минимизировать заданную линейную функцию нескольких переменных при заданных линейных ограничениях на переменные.
Это и есть постановка задачи ЛП в самом общем виде. При этом под линейным ограничением понимается любое линейное уравнение или линейное неравенство.
Функция, которую требуется максимизировать (минимизировать), называется
целевой функцией задачи.
Любой набор значений всех переменных задачи ЛП называется планом задачи. План, удовлетворяющий всем ограничениям задачи, называется допустимым. Допустимый план, на котором достигается наибольшее (наименьшее) среди всех допустимых планов значение целевой функции, называется оптимальным.
Решить задачу ЛП – это значит найти ее оптимальный
план ![]() и соответствующее значение целевой
функции
и соответствующее значение целевой
функции ![]() или доказать, что оптимальных планов нет.
или доказать, что оптимальных планов нет.
Задачу ЛП в общей постановке всегда можно свести к любой из двух следующих форм (частных случаев общей задачи ЛП).
Стандартная задача ЛП:
![]() (14)
(14)
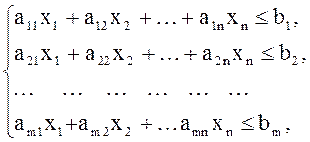 (15)
(15)
![]() . (16)
. (16)
Каноническая задача ЛП:
![]() (17)
(17)
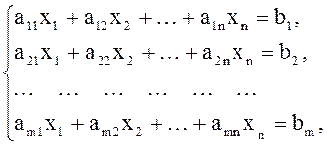 (18)
(18)
![]() (19)
(19)
Эти две формы задачи ЛП удовлетворяют следующим условиям:
1. В качестве направления оптимизации в них выбрана максимизация целевой функции.
2. В ограничениях присутствуют требования неотрицательности (16) и (19) для всех переменных задачи.
3. Все остальные ограничения, кроме требования неотрицательности всех переменных, однотипны: линейные неравенства (15) – в стандартной задаче, линейные равенства (18) – в канонической.
Замечание. Любое неравенство со знаком ![]() можно
преобразовать в эквивалентное ему неравенство со знаком
можно
преобразовать в эквивалентное ему неравенство со знаком ![]() , умножая обе части неравенства на множитель
(-1). Поэтому без ограничения общности можно считать, что все неравенства в
ограничениях задачи ЛП имеют знак
, умножая обе части неравенства на множитель
(-1). Поэтому без ограничения общности можно считать, что все неравенства в
ограничениях задачи ЛП имеют знак ![]() (или, наоборот, все
неравенства имеют знак
(или, наоборот, все
неравенства имеют знак ![]() ).
).
Чтобы добиться выполнения условия 1 задачу минимизации
целевой функции ![]() заменяют на задачу максимизации
функции
заменяют на задачу максимизации
функции
![]() при тех
же ограничениях на переменные. Легко проверяется (проделайте это самостоятельно),
что оптимальные планы преобразованной задачи совпадают с оптимальными планами
исходной и при этом
при тех
же ограничениях на переменные. Легко проверяется (проделайте это самостоятельно),
что оптимальные планы преобразованной задачи совпадают с оптимальными планами
исходной и при этом ![]()
Выполнение условия 2
достигается следующим образом: в целевую функцию и все ограничения задачи
вместо каждой переменной ![]() произвольного знака (т. е.
такой, что требование неотрицательности
произвольного знака (т. е.
такой, что требование неотрицательности ![]() отсутствует
среди ограничений) подставляется выражение
отсутствует
среди ограничений) подставляется выражение ![]() для
всех вновь введенных переменных в ограничения вводятся требования
неотрицательности
для
всех вновь введенных переменных в ограничения вводятся требования
неотрицательности ![]() Смысл такой замены очевиден:
число произвольного знака можно представить в виде разности двух
неотрицательных чисел. Ясно, что оптимальные значения
Смысл такой замены очевиден:
число произвольного знака можно представить в виде разности двух
неотрицательных чисел. Ясно, что оптимальные значения ![]() переменных
исходной задачи находятся по формулам
переменных
исходной задачи находятся по формулам ![]() где
где ![]() - оптимальные значения переменных
преобразованной задачи.
- оптимальные значения переменных
преобразованной задачи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.