Если диагональные элементы матрицы А по модулю превосходят
суммы модулей остальных элементов соответствующих строк, то разрешив систему
(1) относительно неизвестных, стоящих по главной диагонали, придем к системе
уравнений вида (3). При этом очевидно, что ![]() ,
определенная равенством (7), будет меньше единицы. Это означает, что
выполняется достаточный признак сходимости простой итерации (как и для
,
определенная равенством (7), будет меньше единицы. Это означает, что
выполняется достаточный признак сходимости простой итерации (как и для ![]() и
и ![]() ).
).
2 способ. Если для системы уравнений не выполнены достаточные условия, то ее можно с помощью линейных комбинаций преобразовать в эквивалентную систему, для которой условия сходимости будут выполнены. Общих правил сведения системы (1) к системе (3), для которой выполнены достаточные условия сходимости итерационного процесса, нет. Линейные преобразования зависят от рассматриваемой системы. Цель преобразования – получить при диагональных членах коэффициенты большие по модулю, т. е. свести систему к 1 способу ( на практике этот способ применяется очень редко).
Пример 1. Найти решение системы
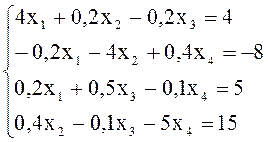
с точностью до 0,001 методом простой итерации.
Решение.
1 этап. Приведение данной системы к виду (3).
Так как диагональные элементы матрицы данной системы по модулю превосходят сумму модулей остальных элементов соответствующих строк, то метод простой итерации в этом случае сходится. Разрешая систему относительно неизвестных, стоящих на диагонали, получаем
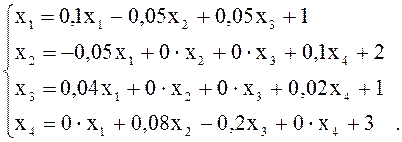
2 этап. Расчетную формулу ![]() в данном случае можно
представить в виде
в данном случае можно
представить в виде
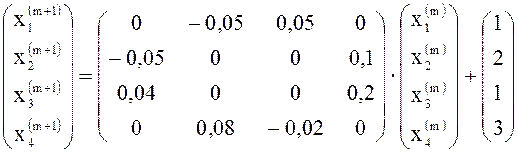
или
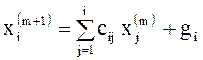 , где i=1, 2, 3, 4.
, где i=1, 2, 3, 4.
Примем в качестве начального приближения 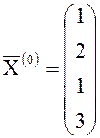 . Полученные
результаты вычислений поместим в табл. 1.
. Полученные
результаты вычислений поместим в табл. 1.
Таблица 1
|
Номер прибли-жения |
Значения неизвестных |
|||
|
|
|
|
|
|
|
1 |
1,1500 |
2,2500 |
1,1000 |
3,1400 |
|
2 |
1,1675 |
2,2565 |
1,1088 |
3,1580 |
|
3 |
1,1682 |
2,2574 |
1,1099 |
3,1584 |
|
4 |
1,1684 |
2,2574 |
1,1099 |
3,1584 |
Норма разности между 3-м и 4-м приближением
![]() .
.
Следовательно, процесс итерации закончен и
![]() .
.
Пример 2. Пусть дана система
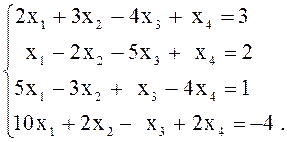 (11)
(11)
Решение. 1 этап. Здесь нет преобладания диагональных элементов. Достаточные условия сходимости итерационного процесса для этой системы не выполнены. Произведем такие линейные преобразования, чтобы было преобладание коэффициентов на главной диагонали. Сначала выпишем те уравнения, в которых имеется преобладание некоторых коэффициентов
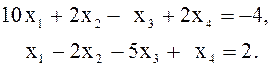
Не
достает еще двух уравнений с преобладанием коэффициентов у ![]() . Постараемся их получить с помощью
линейных преобразований. Вычтем из первого уравнения второе:
. Постараемся их получить с помощью
линейных преобразований. Вычтем из первого уравнения второе: ![]() - второе уравнение. Умножим первое и
третье уравнение системы (1) на два и сложим, а затем вычтем второе и четвертое
уравнения. В результате получим
- второе уравнение. Умножим первое и
третье уравнение системы (1) на два и сложим, а затем вычтем второе и четвертое
уравнения. В результате получим ![]() - четвертое уравнение.
- четвертое уравнение.
Система будет выглядеть следующим образом:
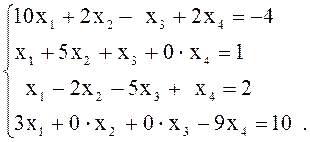
К этой системе может быть применен метод простой итерации, т. к. коэффициенты на главной диагонали преобладают.
2. Метод Зейделя
Пусть система линейных алгебраических уравнений (1),
как и в методе простой итерации, приведена в результате линейных преобразований
к виду (3). Систему (3) будем решать методом последовательных приближений
следующим образом: при вычислении (k+1) приближенного значения
неизвестной ![]() при
при ![]() используются
уже вычисленные ранее (k+1) приближения неизвестных
используются
уже вычисленные ранее (k+1) приближения неизвестных ![]() и
(k) – приближения неизвестных
и
(k) – приближения неизвестных ![]() .
Таким образом, если задан начальный вектор решения
.
Таким образом, если задан начальный вектор решения ![]() системы
(1), то нахождение ее первого приближенного решения методом Зейделя ведется по
формулам:
системы
(1), то нахождение ее первого приближенного решения методом Зейделя ведется по
формулам:
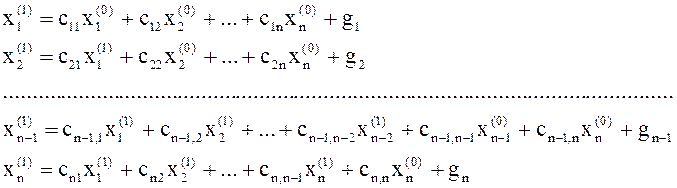 (12)
(12)
Аналогично (k+1) – приближенное решение, которое находится по формуле
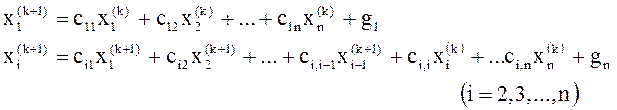 (13)
(13)
или
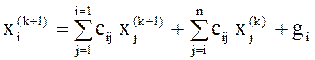 .
.
Запишем систему уравнений (13) в матричной форме
![]() , (14)
, (14)
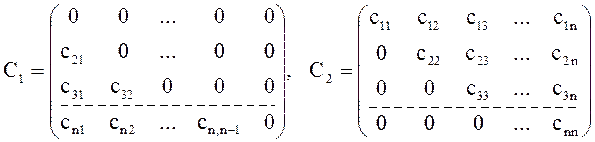 ,
,
причем
матрица С,входящая в уравнение (4), равна сумме ![]() и
и ![]() :
: ![]() .
.
Из системы (14) находим ![]()
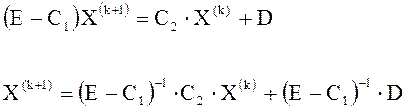 (15)
(15)
Из выражения (15) видно, что метод Зейделя эквивалентен некоторому методу
простой итерации, поэтому для его сходимости при любом начальном приближении
необходимо и достаточно, чтобы все собственные значения матриц ![]() по модулю были меньше единицы. Области
сходимости у метода Зейделя и метода итерации разные. Поэтому при сходимости
одного метода другой может не сходиться и о быстроте тоже ничего определенного
сказать нельзя. Достаточный признак сходимости у обоих методов один и тот же,
т. е. какая-либо из норм (для метода Зейделя
по модулю были меньше единицы. Области
сходимости у метода Зейделя и метода итерации разные. Поэтому при сходимости
одного метода другой может не сходиться и о быстроте тоже ничего определенного
сказать нельзя. Достаточный признак сходимости у обоих методов один и тот же,
т. е. какая-либо из норм (для метода Зейделя ![]() )
меньше единицы. На практике итерационный процесс по методу Зейделя
заканчивается, если разность между двумя соседними приближениями по норме
становится меньше заданной
)
меньше единицы. На практике итерационный процесс по методу Зейделя
заканчивается, если разность между двумя соседними приближениями по норме
становится меньше заданной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.