Алгебра векторов

1.  Алгебра векторов.

В науке рассматриваются объекты разной природы. Некоторые из этих объектов характеризуются только своим численным значением (объем, температура, масса и т.д.). Такие объекты называются скалярными величинами. Для описания других объектов необходимо задавать не только их численное значение, но и направление (сила, скорость и т.д.); такие объекты называются векторными величинами. Существуют объекты еще более сложной природы (тензоры, например).

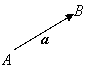В этом разделе мы изучим теорию свободных (геометрических, математических) векторов.

1.1. Основные определения.

Опр. 1.1.1. Вектором называется отрезок, на котором задано направление, т.е. известно, какая из двух конечных точек А, В этого отрезка является началом, какая – концом вектора.

Обозначать векторы принято одним из следующих способов:  (А – начальная точка, В –конечная точка), ,, аи т.д.

Опр. 1.1.2. Нулевым вектором (нуль-вектором) называется вектор, у которого начальная и конечная точка совпадает. Направление нулевого вектора не определяется (считается произвольным). Нуль-вектор будем обозначать 0,  или просто 0.

Опр. 1.1.3. Длиной (модулем, абсолютной величиной) вектора называется расстояние между его начальной и конечной точками. Обозначение: 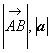. Естественно, .

Опр. 1.1.4. Векторы называются коллинеарными, если они расположены на одной или на параллельных прямых. Другими словами, векторы коллинеарны, если существует прямая, которой они параллельны. Коллинеарность обозначается обычным символом параллельности: a || b. Нуль-вектор коллинеарен любому другому вектору, так как он не имеет определенного направления:

0 || а для а.

Коллинеарные вектора, имеющие одинаковое направление, будем называть сонаправленными. Обозначение сонаправленности: . Противонаправленными будем называть коллинеарные вектора противоположного направления; обозначение: . Очевидны следующие свойства отношений сонаправленности и противонаправленности:

1. Если,, то ;

2. Если,, то ;

3. Если,, то ;

4. Если,, то .

Опр. 1.1.5. Векторы называются компланарными, если существует плоскость, которой они параллельны.

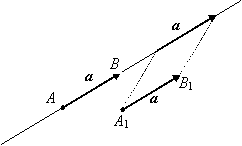
Опр. 1.1.6. Два вектора называются равными, если они коллинеарны, одинаково направлены и имеют равные длины.

Это определение заслуживает того, чтобы объяснить его подробнее, так как именно в нем заключается специфика того, что называется свободными (или геометрическими) векторами. Оно означает, что не имеет значения, из какой точки отложен вектор, т.е. если дан вектор , то он может быть перенесен в любую точку А₁ (для любой точки А₁ может быть построен, и притом единственным способом, вектор , равный вектору ). Таким образом, на рисунке справа изображены не три вектора, а три раза изображен один и тот же вектор.